THE NATURE OF MOLECULAR RECOGNITION, SELF-ASSEMBLY AND SELF-ORGANIZATION: REVISED INFORMATION THEORY AND THE RELATION OF ENTROPY, SYMMETRY AND DIVERSITY

Shu-Kun Lin

Molecular Diversity Preservation International (MDPI), Sangergasse 25, Basel CH-4054 Switzerland. http://www.mdpi.org/lin, e-mail: [email protected]

Molecular interactions seek the most symmtric static structures. However, symmetry has been mainly regarded as a mathematical attribute [1-2]. Curie-Rosen symmetry principle [2] ] is a higher symmetry- higher stability relation that has been seldom, if ever, accepted for consideration of structural stability and process spontaneity (or process irreversibility). Most people accept the higher symmetry-lower entropy relation because entropy is a degree of disorder and symmetry has been erroneously regarded as order [3].

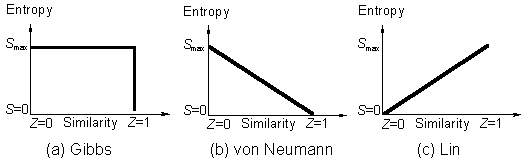
Some authors realized that, it is necessary to consider information and its conversion, in addition to material, energy and their conversions [4]. I have substantially modified information theory with three laws of information theory given and the similarity principle (entropy increases monotonically with the similarity of the concerned property among the components (fig. 1) [5]) proved. Symmetry principle has been proved as a special case of similarity principle. The structural stability criteria of symmetry maximization can be applied to alll kinds of symmetry evolution. Several concepts and their quantitative relation are set up: the higher symmetry, higher similarity, higher entropy, less information and less diversity and they are all related to higher stability.

Figure 1. (a) Correlation of entropy (ordinate) of mixing with similarity (abscissa) according to Gibbs where entropy of mixing suddenly becomes zero if the components are indistinguishable according to the Gibbs paradox (http://mdpi.org/entropy/entropyweb/gibbs-paradox.htm). Entropy decreases discontinuously. Figure 1a expresses Gibbs paradox statement of "same or not the same" relation. (b) von Neumann: the entropy of mixing decreases continuously with the increase in the property similarity. (c) Entropy increases continuously according to the present author [5] (not necessarily a straight line because the similarity can be defined in different ways).

Finally, to have some fun I conclude that symmetry is in principle ugly. It may be related to the perception of beauty only because it contributes to stability.

Definitions

Symmetry and Nonsymmetry: Symmetry as a Greek word means same measure [1] or indistinguishability measure. Imperfect symmetry can be measured by similarity, instead of indistinguishability. Nonsymmetry is a measure of difference or distinguishability.

Entropy and Information: Entropy S of the structure regarding the property X is given by the following familiar Gibbs-Shannon expression [5]

(1)
with the understanding that  and . Because  and , entropy is nonnegative (). If the w microstates have the same value of the considered property, hence the same value of ,
(2)
where the maximal entropy is denoted as L, because
(3)
(Gibbs inequality, see [5d] and the relevant citations).

A new logarithmic function L can be defined as the sum of entropy S and information I:

(4)
For example, a 1.44MB floppy diskette, whether the disk is empty or occupied with a file of the size of 1.44MB or not. Let us use any available compression method to reduce the size of the original file to 0.40MB. Then, and and .

The Three Laws and the Stability Criteria

Similar to the laws in thermodynamics, we have

The first law of information theory: the logarithmic function L (, or the sum of entropy and information,) of an isolated system remains unchanged.

The second law of information theory: Information I of an isolated system decreases to a minimum at equilibrium. Or: for an isolated system, entropy S increases to a maximum at equilibrium.

For other systems (closed system or open system), we define universe = system + surroundings and treat the universe formally as an isolated system. Then, these two laws are expressed as the following: The function L of the universe is a constant. The entropy S of the universe tends toward a maximum. Therefore, the second law of information theory can be used as the criteria of structural stability and process spontaneity (or process irreversibility) in all cases, whether they are isolated systems or not. If the entropy of system + surroundings increases from structure A to structure B, B is more stable than A. The higher the value  for the final structure is, the more spontaneous (or more irreversible) the process will be. The second law of thermodynamics is a special case of the second law of information theory.

The third law of information theory: For a perfect crystal (at zero absolute thermodynamic temperature), the information is zero and the static entropy is the maximum. Or "for a perfect symmetric static structure, the information is zero and the static entropy is the maximum".

From (3), we can prove the higher-similarity-higher entropy relation and prove the Similarity principle: The higher the similarity among the components is, the higher value of entropy will be and the higher stability will be. The components can be individual molecules, molecular moieties or phases. As a special case of similarity principle, it is clear that the higher the symmetry (indistinguishability)of the structure is, the higher value of entropy will be and the higher stability will be.

Similarity Rule and Complementarity Rule

All intermolecular processes (molecular recognition and molecular assembling or the formation of any kinds of chemical bond) and intramolecular processes (e.g., protein folding) between molecular moieties are governed either by similarity rule or by complementarity rule or both. Similarity rule (a component in a molecular recognition process loves others of alike properties, such as hydrophobic interaction, p-stacking in DNA molecules, similarity in softness of the well-known hard-soft-acid-base rules) predicts the affinity of individuals of similar properties. It follows the similarity principle.

On the contrary, complementarity rule predicts the affinity of individuals of certain contrast properties. Both types of rule still remain strictly empirical. Suppose there are n kinds of property X, Y, Z, ..., etc. (See the definition of entropy and labeling) and . For a binary system, if the two individuals are contrast in l kinds of property (negative charge-positive charge, donor-acceptor, convex and concave, etc.) and exactly the same for the rest m kinds of property, the relation of these two components are complementary. For interactions following complementarity rule, the final structure is more "complete", more integral, and more symmetric due to the property offset of the components. After the offset, the two components at the interface are more similar in property.

ABC + ABC = ABC

Figure 2. The print and the imprint (or ligand and target molecules) [4b] are complementary. The final structure is more symmetric.
 We should emphasize that similarity rule is always more significant than complementarity rule, because most properties of the complementary components are the same or very similar. Examples in chemistry is the HSAB (hard-soft-acid-base) rule where the two components (acid and base) should be similar softness or similar hardness (see any modern texts in inorganic chemistry). Another example is the complementary pair of LUMO (lowest unoccupied molecular orbital) and HOMO (highest occupied MO) where the energy levels of the MO are very close (see a modern textbook of organic chemistry). Pauling’s resonance theory for the formation of chemical bond also conforms to the consideration of the similarity and complementarity of the components.

Is Symmetry Beautiful?

"Symmetry is order" [3] and "symmetry is beauty" [6] can be very misleading in science [7]. Sometimes, graphic representation might be biased by the authors to create false symmetry (because symmetry is beauty). One example is shown in figure 3.

Figure 3. Stereochemical representation with false mirror symmetry: Both wedges have the thick ends at R3 and R4 placed identically away from the center [8].
  The symmetric fullerene C60 is beautiful. However, many derivatives of C60 have been synthesized by organic chemists. These derivatives are less symmetric, more difficult to produce and more significant. None of the drugs (pharmaceuticals) discovered so far is very symmetric. Very few bioactive compounds are very symmetric. Because all the most important molecules of life, such as amino acids, sugars, and nucleic acids, are asymmetric, we may also attribute beauty to those objects that are practically more difficult to create and practically more significant. The highest symmetry means equilibrium in science and death in life.

Conclusion

All chemical reactions leading to the formation of stable macro- and supramolecular architectures follow similarity rules and complementarity rules. The stability and the observed structural symmetry provided rich evidence for the validity of the revised information theory, particularly the third law of the information theory.

Acknowledgements

The author is very grateful to Dr. Peter Ramberg, Dr. S. Anand Kumar, Dr. Alexey V. Eliseev and Dr. Jerome Karle and numerous other colleagues for their kind invitations to give lectures on the similarity principle and the topics of ugly symmetry and beautiful diversity.

References

1. Hargittai, I. (1994) Symmetry, A Unifying Concept, Shelter Publications, Inc., Bolinas, California

2. Rosen, J. (1995) Symmetry in Science, Springer: New York. (b) Rosen, J. (1983) A Symmetry Primer for Scientists, Wiley: New York. (c) Lin, S.-K. (1999) Entropy, 1, 53-54 (http://www.mdpi.org/entropy/htm/e1030053.htm)

3. (a) Prigogine, I. Stengers, I. (1984) Order out of Chaos, Heinemann, London. (b) Kondepudi, D. and Prigogine, I. (1998) Modern Thermodynamics: From Heat Engines to Dissipative Structures. Wiley: Chichester, UK, chapters 19-20; Book review: Lin, S. -K. (1999) Entropy, 1, 148-149 (http://www.mdpi.org/entropy/htm/e1040148.htm)

4. Lehn, J. M. (2001) Some Reflections on Chemisry-Molecular, Supramolecular and Beyond, in: Keinan, E. & Schechter, I. (Eds.) Chemistry for the 21st Century, Wiley-VCH: Weinheim, p1-7. (b) Günter, W. (2000) Templated Synthesis of Polymers – Molecularly Imprinted Materials for Recognition and Catalysis. In Diederich, F. & Stang, P. J. (editors) Templated Organic Synthesis, Wiley-VCH: Weinheim, pp39-73

5. (a) Lin, S.-K. (1997) Theorochem J. Mol. Struct.398, 145-153. ( (b) Lin, S.-K. (1996) EJ. Theor. Chem. 1, 135-150 (c) Lin, S.-K. (1996) Molecules, 1, 57-67. (d) Lin, S.-K. (1996) J. Chem. Inf. Comp. Sci. 36, 367-376. (www.mdpi.org/lin/lin-rpu.htm)

6. (a) Perrett, D. I.; May, K. A.; Yoshikawa, S. (1994) Nature 368, 239-241; (b) Enguist, M.; Arak, A. (1994) Nature 372, 167-175
  1. Lin, S. -K. (1999) Ugly Symmetry. Invited lecture at the 218th ACS national meeting in New Orleans, Louisiana, August 22-26, 1999 (http://mdpi.org/lin/uglysym1.htm)
  2. Lin, S. K., Patiny, L., Yerin, A., Wisniewski, J. L. & Bernard Testa, T. (2000) One-Wedge Convention for Stereochemical Representations. Enantiomer, 5, 571-583. (http://www.unibas.ch/mdpi/molecules/wedge/)