Since heat was first used as a motive power in the steam-engine, thereby suggesting from practice that a certain quantity of work may be treated as equivalent to the heat needed to produce it, it was natural to assume also in theory a definite relation between a quantity of heat and the work which in any possible way can be produced by it, and to use this relation in drawing conclusions about the nature and the laws of heat itself. In fact, several fruitful investigations of this sort have already been made; yet I think that the subject is not yet exhausted, but on the other hand deserves the earnest attention of physicists, partly because serious objections can be raised to the conclusions that have already been reached, partly because other conclusions, which may readily be drawn and which will essentially contribute to the establishment and completion of the theory of heat, still remain entirely unnoticed or have not yet been stated with sufficient definiteness.
The most important of the researches here referred to was that of S. Carnot, and the ideas of this author were afterwards given analytical form in a very skillful way by Clapeyron. Carnot showed that whenever work is done by heat and no permanent change occurs in the condition of the working body, a certain quantity of heat passes from a hotter to a colder body. In the steam-engine, for example, by means of the steam which is developed in the boiler and precipitated in the condenser, heat is transferred from the grate to the condenser. This transfer he considered as the heat change, corresponding to the work done. He says expressly that no heat is lost in the process, but that the quantity of heat remains unchanged, and adds: "The fact is not doubted; it was assumed at first without investigation, and then established in many cases by calorimetric measurements. To deny it would overthrow the whole theory of heat, of which it is the foundation." I am not aware, however, that it has been sufficiently proved by experiment that no loss of heat occurs when work is done; it may perhaps, on the contrary, be asserted with more correctness that even if such a loss has not been proved directly, it has yet been shown by other facts to be not only admissible, but even highly probable. If it be assumed that heat, like a substance, can not diminish in quantity, it must also be assumed that it can not increase. It is, however, almost impossible to explain the heat produced by friction except as an increase in the quantity of heat. The careful investigations of Joule, in which heat is produced in several different ways by the application of mechanical work, have almost certainly proved not only the possibility of increasing the quantity of heat in any circumstances but also the law that the quantity of heat developed is proportional to the work expanded in the operation. To this it must be added that other facts have lately become known which support the view, that heat is not a substance, but consists in a motion of the least parts of bodies. If this view is correct, it is admissible to apply to heat the general mechanical principle that a motion may be transformed into work, and in such a manner that the loss of kinetic energy is proportional to the work accomplished.
These facts, with which Carnot also was well acquainted and the importance of which he has expressly recognized, almost compel us to accept the equivalence between heat and work, on the modified hypothesis that the accomplishment of work requires not merely a change in the distribution of heat, but also an actual consumption of heat, and that, conversely, heat can be developed again by the expenditure of work.
...
If any body changes its volume, mechanical work will in general be either produced or expended. It is, however, in most cases impossible to determine this exactly, since besides the external work there is generally an unknown amount of internal work done. To avoid this difficulty, Carnot employed the ingenious method already referred to of allowing the body to undergo its various changes in succession, which are so arranged that it returns at last exactly to its original condition. In this case, if internal work is done in some of the changes, it is exactly compensated for in the others, and we may be sure that the external work, which remains over after the changes are completed, is all the work that has been done. Clapeyron has represented this process graphically in a very clear way, and we shall follow his presentation now for the permanent gases, with a slight alteration rendered necessary by our principle.

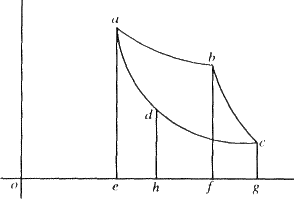
In the figure (Fig. 1), let the abscissa oe represent the volume and the ordinate ea the pressure on a unit weight of gas, in a condition in which its temperature = t. We assume that the gas is contained in an extensible envelope, which, however, cannot exchange heat with it. If, now, it is allowed to expand in this envelope, its temperature would fall if not heat were imparted to it. To avoid this, let it be put in contact, during its expansion, with a body A, which is kept at the constant temperature t, and which imparts just so much heat to the gas that its temperature also remains equal to t. During this expansion at constant temperature, its pressure diminishes according to Mariotte's law, and may be represented by the ordinate of a curve, ab, which is a portion of an equilateral hyperbola. When the volume of the gas has increased in this way from oe to of, the body A is removed, and the expansion is allowed to continue without the introduction of more heat. The temperature will then fall, and the pressure diminish more rapidly than before. The law which is followed in this part of the process may be represented by the curve bc. When the volume of the gas has increased in this way from of to og, and its temperature has fallen from t to τ, we begin to compress it, in order to restore it again to its original volume oe. If it were left to itself its temperature would again rise. This, however, we do not permit, but bring it in contact with a body B, at the constant temperature τ, to which it at once gives up the heat that is produced, so that it keeps the temperature τ; and while it is in contact with this body we compress it so far (by the amount gh) that the remaining compression he is exactly sufficient to raise its temperature from τ to t, if during this last compression it gives up no heat. During the former compression the pressure increases according to Mariotte's law, and is represented by the portion cd of an equilateral hyperbola. During the latter, on the other hand, the increase is more rapid and is represented by the curve da. This curve must end exactly at a, for since at the end of the operation the volume and temperature have again their original values, the same must be true of the pressure also, which is a function of them both. The gas is therefore in the same condition again as it was at the beginning.
Now, to determine the work produced by these changes, for the reasons already given, we need to direct our attention only to the external work. During the expansion the gas does work, which is determined by the integral of the product of the differential of the volume into the corresponding pressure, and is therefore represented geometrically by the quadrilaterals eabf and fbcg. During the compression, on the other hand, work is expended, which is represented similarly by the quadrilaterals gcdh and hdae. The excess of the former quantity of work over the latter is to be looked on as the whole work produced during the changes, and this is represented by the quadrilateral abcd.
If the process above described is carried out in the reverse order, the same magnitude, abcd, is obtained as the excess of the work expended over the work done.
...
Carnot assumed, as has already been mentioned, that the equivalent of the work done by heat is found in the mere transfer of heat from a hotter to a colder body, while the quantity of heat remains undiminished.
The latter part of this assumption--namely, that the quantity of heat remains undiminished--contradicts our former principle, and must therefore be rejected if we are to retain that principle. On the other hand, the first part may still obtain in all its essentials. For though we do not need a special equivalent for the work done, since we have assumed as such an actual consumption of heat, it still may well be possible that such a transfer of heat occurs at the same time as the consumption of heat, and also stands in a definite relation to the work done. It becomes important, therefore, to consider whether this assumption, besides the mere possibility, has also a sufficient probability in its favor.
A transfer of heat from a hotter to a colder body always occurs in those cases in which work is done by heat, and in which also the condition is fulfilled that the working substance is in the same state at the end as at the beginning of the operation. Yet, in order to establish a relation between the heat transferred and the work done, a certain restriction is necessary. For since a transfer of heat can take place without mechanical effect if a hotter and a colder body are immediately in contact and heat passes from one to the other by conduction, the way in which the transfer of a certain quantity of heat between two bodies at the temperatures t and τ can be made to do the maximum of work is so to carry out the process, as was done in the above cases, that two bodies of different temperatures never come in contact.
It is this maximum of work which must be compared with the heat transferred. When this is done it appears that there is in fact ground for asserting, with Carnot, that it depends only on the quantity of the heat transferred and on the temperatures t and τ of the two bodies A and B, but not on the nature of the substance by means of which the work is done. This maximum has, namely, the property that by expending it as great a quantity of heat can be transferred from the cold body B to the hot body A as passes from A and B when it is produced. This may easily be seen, if we think of the whole process formerly described as carried out in the reverse order, so that, for example, in the first case the gas first expands by itself, until its temperature falls from t to τ, is then expanded in connection with B, is then compressed by itself until its temperature is again t, and finally is compressed in connection with A. In this case more work will be employed during the compression than is produced during the expansion, so that on the whole there is a loss of work, which is exactly as great as the gain of work in the former process. Further, there will be just as much heat taken from the body B as was before given to it, and just as much given to the body A as was before taken from it, whence it follows not only that the same amount of heat is produced as was formerly consumed, but also that the heat which in the former process was transferred from A to B now passes from B to A.
If we now suppose that there are two substances of which the one can produce more work than the other by the transfer of a given amount of heat, or, what comes to the same thing, needs to transfer less heat from A to B to produce a given quantity of work, we may use these two substances alternately by producing work with one of them in the above process. At the end of the operations both bodies are in their original condition; further, the work produced will have exactly counterbalanced the work done, and therefore, by our former principle, the quantity of heat can have neither increased nor diminished. The only change will occur in the distribution of the heat, since more heat will be transferred from B to A than from A to B, and so on the whole heat will be transferred from B to A. By repeating these two processes alternately it would be possible, without any expenditure of force or any other change, to transfer as much heat as we please from a cold to a hot body, and this is not in accord with the other relations of heat, since it always shows a tendency to equalize temperature differences and therefore to pass from hotter to colder bodies.
It seems, therefore, to be theoretically admissible to retain the first and the really essential part of Carnot's assumptions, and to apply it as a second principle in conjunction with the first; and the correctness of this method is, as we shall soon see, established already in many cases by its consequences.
...
Annalen der Physik und Chemie, 125, 353- (1865) [translated and excerpted in William Francis Magie, A Source Book in Physics [New York: McGraw-Hill, 1935]
...
We obtain the equation[1] 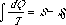 which, while somewhat differently arranged, is
the same as that which was formerly used to determine S.
which, while somewhat differently arranged, is
the same as that which was formerly used to determine S.
If we wish to designate S by a proper name we can say of it that it is the transformation content of the body, in the same way that we say of the quantity U that it is the heat and work content of the body. However, since I think it is better to take the names of such quantities as these, which are important for science, from the ancient languages, so that they can be introduced without change into all the modern languages, I proposed to name the magnitude S the entropy of the body, from the Greek word η τροπη, a transformation. I have intentionally formed the word entropyso as to be as similar as possible to the word energy, since both these quantities, which are to be known by these names, are so nearly related to each other in their physical significance that a certain similarity in their names seemed to me advantageous.
...
Finally I may allow myself to touch on a matter whose complete treatment would not be in place here, because the statements necessary for that purpose would take up too much room, but of which I believe that even the following short indication will not be without interest, in that it will contribute to the recognition of the importance of the quantities which I have introduced into the formulation of the second law of the mechanical theory of heat. The second law, in the form which I have given it, states the fact that all transformations which occur in nature occur in a certain sense which I have taken as positive, of themselves, that is, without compensation, but that they can only occur in the opposite or negative sense in such a way that they are compensated by positive transformations which occur at the same time. The application of this law to the universe leads to a conclusion to which W. Thomson first called attention and about which I have already spoken in a recently published paper. This conclusion is that if among all the changes of state which occur in the universe the transformations in one sense exceed in magnitude those in the opposite sense, then the general condition of the universe will change more and more in the former sense, and the universe will thus persistently approach a final state.
The question now arises whether this final state can be characterised in a simple and also a definite way. This can be done by treating the transformations, as I have done, as mathematical quantities, whose equivalent values can be calculated and united in a sum by algebraic addition.
In my papers so far published I have carried out such calculations with respect to the heat present in bodies and to the arrangement of the constituents of the bodies. For each body there are found two quantities, the transformation value of its heat content and its disgregration, the sum of which is its entropy. This however does not complete the business. The discussion must also be extended to the radiant heat, or otherwise expressed, to the heat transmitted through the universe in the form of advancing vibrations of the ether, and also to such motions as cannot be comprehended under the name heat.
The treatment of these latter motions, at least as far as they are the motions of ponderable masses, can be briefly settled, since we come by a simple argument to the following conclusion: If a mass, which is so great that in comparison with it an atom may be considered as vanishingly small, moves as a whole, the transformation value of this motion is to be looked on as vanishingly small in the same way in comparison with its kinetic energy; from which it follows that if such a motion is transformed into heat by a passive resistance, then the equivalent value of the uncompensated transformation which then occurs is simply represented by the transformation value of the heat produced. The radiant heat, however, cannot be treated so briefly, since there is need still of a certain special treatment in order to find out how its transformation value is to be determined. Although, in the paper which was recently published and to which I have previously referred, I have already discussed radiant heat in its connection with the mechanical theory of heat, yet I have not as yet treated the question which has here come up, since it was then only my purpose to prove that there was no contradiction between the laws of radiant heat and a fundamental law which I assumed in the mechanical theory of heat. I reserve for future consideration the more particular application of the mechanical theory of heat and especially of the law of equivalents of transformation to radiant heat.
For the present I will confine myself to announcing as a result of my argument that if we think of that quantity which with reference to a single body I have called its entropy, as formed in a consistent way, with consideration of all the circumstances, for the whole universe, and if we use in connection with it the other simpler concept of energy, we can express the fundamental laws of the universe which correspond to the two fundamental laws of the mechanical theory of heat in the following simple form.
1. The energy of the universe is constant.
2. The entropy of the universe tends toward a maximum.
 Back to the list of
selected historical papers.
Back to the list of
selected historical papers. Back to the top of Classic
Chemistry.
Back to the top of Classic
Chemistry.