Shu-Kun Lin
Molecular Diversity Preservation International (MDPI), Matthaeusstrasse 11, CH-4057 Basel, Switzerland (e-mail: [email protected], http://www.mdpi.org/lin)
The Similarity Principle:
If all the other conditions remain constant, the higher the similarity among the components of an ensemble (or a considered system) is, the higher value of entropy of the mixture (for fluid phases) or the assemblage (for a static structure or a system of solid phase) or any other structure (such as an ensemble of quantum states in quantum mechanics) will be, the more stable the mixture or the assemblage will be, and the more spontaneous the process leading to such a mixture or assemblage will be.This theory [1] is very useful for characterizing structural stability and process spontaneity. For example, it is applied to the phase separation as a simple rule: If one wants to mix substances, increase their similarity (of relevant properties); if one plans to separate the substances as phases, reduce their similarity! Then, the desirable processes of mixing or separation will happen spontaneously. In chemistry and physics, by changing temperature and pressure, one can control the similarity and in turn, the system will go to the desired direction (e.g., phase separation or homogeneous mixture formation). Higher temperature and pressure may lead to higher similarity. This theory is important in understanding molecular recognition, self-organization, molecular assembling and molecular replication.

Experimental Facts: (a) Phase separation. Different substances do
not
mix but spontaneously separate because the indistinguishable substances
are the most spontaneously miscible ones. As a consequence of the most
spontaneously mixing the most similar (indistinguishable) substances,
different
substances separate. (b) Chemical bond formation or Pauling's resonance
(mixing of the quantum states). (c) Information registration process (![]() )
is a process of assembling different species. (d) All
symmetry-breaking
phenomena also indicate that the assembling of indistinguishable
subsystems is the most spontaneous process leading to the most
stable state.
)
is a process of assembling different species. (d) All
symmetry-breaking
phenomena also indicate that the assembling of indistinguishable
subsystems is the most spontaneous process leading to the most
stable state.
Theoretical Arguments: (a) From the well-known inequality
From (1),
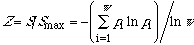 (3)
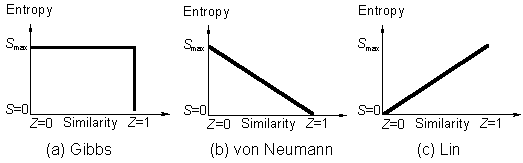
(3)Entropy also increases with the symmetry. Given two systems which are identical in material contents, energies, and all the other properties except their symmetries which are the only difference. Which system would be more stable, the one with higher symmetry or the one with lower symmetry? For a solid phase, is the crystalline structure or the non-crystalline structure more stable?
In answering this structural relative stability question, the entropy S is a pertinent thermodynamic function to consider. However, according to "higher symmetry-higher orderliness-less entropy-less stability" relation in all statistical mechanics (see references cited in ref. [1a]), such as the treatment of the Ising model of symmetry breaking problems, higher symmetry in a system would imply a lower value of S, and the answer would be that the less symmetrical static structure is more stable. This is incorrect and does not conform to the experimental observation (also read my comments in [3]).
Curie's symmetry principle says "the symmetry group of the cause is a subgroup of the symmetry group of the effect" [2]. Semantically, the Greek word symmetry means same measure or indistinguishability measure.The Curie-Rosen symmetry principle [2] can be proved [1h] by the similarity principle and it is correct.
A logarithmic relation (eq 4) has been established [1a] which
conforms
to Curie's symmetry principle [2]. For a system of w
microstates,
References and Notes:
1. (a) Lin, S.-K. Correlation
of entropy with similarity and symmetry.
J.
Chem. Inf. Comp. Sci. 1996, 36, 367-376. (b) Lin,
S.-K.
Gibbs paradox of entropy
of mixing: experimental facts, its rejection and
the theoretical consequences. Electronic
Journal of Theoretical Chemistry. 1996, 1,
135-150; (c) Lin, S. -K. Molecular
diversity assessment: Logarithmic relations
of information and species diversity and logarithmic relations of
entropy
and indistinguishability after rejection of Gibbs paradox of entropy of
mixing. Molecules 1996, 1, 57-67. (d) Lin,
S.-K. Understanding
structural stability and process spontaneity based on the rejection of
the Gibbs paradox of entropy of mixing. Theochem–J. Mol. Struc.
1997,
398,
145-153. (e) Lin, S.-K. Symmetry breaking problem resolved
(American
Physical Society Meeting, Kansas City, MO, March 17-21, 1997).
Bull.
Am. Phys. Soc. 1997, 42, 679. (f) Lin, S.-K.
The nature
of the chemical process. A new information theory. The 36th IUPAC
Congress,
Geneva, Switzerland, August 17-22, 1997. Chimia 1997, 51,
515. (g) Lin, S.-K. Similarity
rule and complementarity rule, Chimia 1999,
53,
383. (http://www.mdpi.org/lin/basel99.htm) (h) Lin, S. -K. The
Nature of the Chemical Process. 1. Symmetry Evolution –Revised
Information
Theory, Similarity Principle and Ugly Symmetry. Int. J. Mol.
Sci.
2001,
2,
10-39. (i) Lin, S.-K. Gibbs
Paradox
and the Concepts of Information, Symmetry, Similarity and
Their Relationship. Entropy 2008, 10, 1-5. DOI:
10.3390/entropy-e10010001.
arXiv:0803.2571. (j) Lin,
S.-K. Gibbs Paradox and
Similarity Principle. Paper presented at MaxEnt2008. 2008, arXiv:0807.4314v1
[physics.gen-ph].
2. (a) Rosen, J. Symmetry in Science; Springer: New York, 1995. See a book review. (b) Rosen, J. The Symmetry Principle. Entropy, 2005, 7(4), 308-313.
3. Lin, S. -K. Lecture entitled "Ugly Symmetry" at many universities
and international conferences. E.g., Ugly
Symmetry, at the 218th ACS National Meeting August 22-26, 1999,
New Orleans, Louisiana. (http://www.mdpi.org/lin/uglysym1.htm). A
longer version: link.