Molecules 2001, 6, 915-926
molecules
ISSN 1420-3049
A New Effective Algorithm for the Unambiguous Identification of the Stereochemical Characteristics of Compounds During Their Registration in Databases
T. Cieplak1 and J.L. Wisniewski2,3,*
1 Cieplak Consulting, Sulzbach, Germany, e-mail: [email protected]
2 MDL Information Systems GmbH, Frankfurt/Main, Germany
3 Pedagogical University, Slupsk, Poland
* Author to whom correspondence should be addressed; e-mail: [email protected]
Received: 15 July 2001 / Accepted: 24 October 2001 / Published: 31 October 2001
Abstract: A new effective algorithm for handling of geometry at chiral centres for the processing of stereochemical structures during their unambiguous registration in databases was designed, programmed and implemented. The chemical and mathematical reasoning behind the algorithm are discussed in detail. Its advantages- in comparison to the methods used so far - are illustrated for the manual as well as for the computer-assisted assignment of stereodescriptors based on the CIP ranking procedure.
Keywords: Stereochemistry; CIP; Stereodescriptors; Determinant algorithm; Chirality
Introduction
Chemical structures represent separate entities, which exist in nature or can be synthesized, and are widely studied and described in publications. A variety of methods have been devised to impart information on the structural representation of compounds. These methods include the use of molecular formulae, various line notations [1], trade/trivial names, registry numbers, structure diagrams, and systematic nomenclature [2].
For the practising chemist, the most acceptable visual representation of a chemical compound is a two-dimensional plan of the three-dimensional structure, and this usually gives an adequate view of the structure, and is easily understood, drawn and copied. Used in reaction sequence it shows clearly the course of the reaction, with display of transient intermediates if required. If it is necessary to show the third dimension, the use of special bond configurations representing lines going above or below the plane can accomplish this. This diagrammatic representation is usually referred to as a structure diagram or structure graph. The structure diagram conventions are established as an international standard and so far are the only unique method of communicating information on a chemical compound. The diagrams, for computer processing, are transformed (manually or automatically) into linear string of characters or into two-dimensional matrices listing all the atoms (nodes) and their mutual interconnections (bonds, edges). These concise representations are referred to as connection tables (CT). Although important only for computer storage and processing, connection tables have, in recent times, been the main means of communication of the information on chemical compounds [3]. Uniquely derived from the standardised structure diagrams, the CT-s became the most complete structural representation and, in the same time, the most visually unrecognisable for the human and the most computer-friendly.
One of the main purposes of the various representations of chemical structures is their unambiguous identification and unique registration for storage in databases of chemical substances as well as for their effective and fast retrieval from the databases. The issue of reliable identification is more and more crucial as database sizes grow steadily. Thus the two biggest and most important databases i.e., CAS and Beilstein contain enormous number of structures (CAS over 18,1 million organic and inorganic substances as of June 2001 [4], and Beilstein File over 8 million organic compounds and 1.4 million inorganic and organometallic compounds as of June 2001 [5]) together with much bigger numbers of accompanying records describing chemical, physical, and recently, also biological characteristics of the corresponding compounds (for example the Beilstein File contains over 35 million associated chemical property and bioactivity records as of June 2001).
The data stored in the databases come from two main sources namely from scientific journals as well as from published patents. For both sources - if they contain structural diagrams representing the compounds - usually some sort of an “offline” graphical structure editing software package is used. The structural diagram of the new compound selected for registration in a database is drawn using a structure editor (ISIS/Draw, Beilstein SE, ChemDraw ACD/ChemSketch, etc.), the resulting - initial - representation of the structural diagram as a connection table is sent as input to a dedicated program for normalisation and afterwards, also as connection table, is stored as a record in the database. The connection table - as referred to in this paper – is understood as a labelled graph for which nodes are stored either as atom adjacency matrices of bond order labels (single, double, triple, single up, single down, etc.) or as an atom adjacency lists which, for each atom separately, contain bond order labels only to directly connected atoms (neighbours). For both representations each atom is specified by the atom property vector containing such information as atomic number, atomic mass (if non-standard), charge, valency (in non standard), etc. Such connection tables are then canonicalized, i.e., a canonical numbering of atoms is generated by special algorithms [6,7]. The only purpose of the canonicalization is to generate - independent of the used structure coding method – a numeric or alphanumeric identifier (strictly numeric for the Beilstein File, for example) which uniquely and unambiguously labels the structural diagram of the input compound. Such an identifier – specific within a particular database - is called a registry number (CRN for CAS or BRN for Beilstein).
An important property of a chemical compound is its stereoisomerism, i.e., the differentiation of the compounds exclusively due to the arrangement of their atoms in space. Different stereoisomers of the same compound should have different registry numbers. This is not always the case since the translation of the stereoisomers into unique registry numbers is a very complex.
This paper describes a new algorithm for analysis and processing of a chemical structure represented as structural graphs in scientific journal and/or patent publications. Correct and unique interpretation of the steric information contained in graphs of such structures – by the computer programs - provides for reliable registration of different stereoisomers of the same compound in databases of chemical compounds.
Representation of the spatial configuration of a chemical structure
In 1859 August Kekulé found that carbon atom is quadrivalent and formulated the basic rules of structural description. In 1874 Van’t Hoff and Lebel introduced, independently of each other, the theory of spatial bond arrangement for tetrahedral carbon atoms [8]. Their theory was soon confirmed by data from chemical and physical experiments and the concept of stereochemistry was born. Since then the need to represent 3D models of compounds using 2D structural diagram conventions has arisen.
The 2D graphical representation of stereoisomers is unambiguous. Even for such strictly formalised representation as in the Beilstein File there are cases of compounds with stereochemical unspecified centres even though all the chiral centres were originally (in the source literature) determined. The graphical representation of structures in the Beilstein File was statistically analysed for a sample of over 3.1 million structures [9] showing relevant difficulties in avoiding ambiguity.
The problem was very recently recognised and in 1996, IUPAC published recommendations for graphic representation of three-dimensional structures [10]. However, these recommendations have received very little attention by organic chemists and database companies and contributed very little to overcoming the confusion and ambiguity. A very interesting recent suggestion by Lin et al. [11] proposing a single wedge convention for chirality representation has relevant advantages over the currently used two wedge (solid and broken) representation and seems to offer the solution and deservedly is getting more and more recognition [12]
It should be noted, however, that stereochemistry is not limited only to chirality as assumed so far. Another important spatial isomerism considered in chemistry is the so called geometrical isomerism resulting from blocked rotation at multiple bonds. The simplest compound occurring in two isomeric geometrical forms is butene. Other examples of this type are cumulated allene as well as substituted ring systems not exceeding 5 atoms in size.
Stereochemistry and its perception are a challenge for any registration software. The various chiral and geometric isomers should be unambiguously registered under unique registry numbers. The issue is by no means trivial. The stereocentres are selected depending on the type of the stereochemistry present. In practice these are either carbon atoms with 4 varied ligands or trivalent nitrogen with three differentiated ligands. In case of geometrical isomerism the central atom laying in the double bond axis for compounds of the allene type takes over the role of the stereocentre. It became obvious that registration of such stereoisomers cannot be handled without systematic nomenclature based on Cahn-Ingold-Prelog (CIP) system [13]. As the latter associates a pre-defined label (R, S, r, s, 0, or E, Z, e, z) with an atom or bond, it can be used to encode stereochemical characteristics as graph nodes or graph edge attributes. These attributes can be then encoded into the connection table of the compound differentiating it from the other compounds.
The attribute must be first manually assigned or algorithmically calculated using a graphical representation of the compound directly. This calculation is based on an algorithm which depends strongly on the 2D graphical representation of the stereochemistry occurring in a compound. For the above/below plane bonds the solid and broken wedges are used. This wedge representation is in most of the cases unique unless the wedge bond must be located between two directly neighbouring chiral centres. For geometrical isomers on both sides of a double bond no particular descriptor is provided for ligands on both sides of the bond. This is definitely a disadvantage for any computer based registry system. It is not clear if the composition of ligands at both sides of the double bond is consciously chosen or simply accidental. It is particularly unclear if the citation source article describes a racemate or simply ignores the stereochemistry of the compound. Usually, to avoid such situations, structure drawing softwares provide for additional conventions such as drawing wavy bonds in order to visualise the undefined steric character of the bond. Some modern drawing software packages (Beilstein SE, ChemDraw) enable entering and representation - in the resulting CT - of the steric double bonds.
Stereodescriptors for structures to be registered in a database are determined using the CIP ordering sequence convention [13]. For all ligands a, b, c, d at located chiral centre(s) the CIP ordering is used to determine a prioritised ranking of the ligands. The lowest priority ligand is then selected as the reference ligand. The line connecting the chiral centre and the lowest priority ligand determines the reference plane. If transition from the line towards higher priority ligands goes in the clockwise direction then the chiral centre is described as R (rectus) otherwise as S (sinister).
The rules as originally suggested by Cahn, Ingold, and Prelog and their extensions and revisions [14,15,16] play a double role. First, they allow determining if the considered atom is really asymmetric, and second they rank the ligands connected to the asymmetric atom producing the pre-defined sequence starting at the least important ligand and ending at the most important one. This ranking and resulting sequence should be unique and always the same. It is well known fact that it is not always true. The CIP rules, even after multiple revisions coming from both chemists and mathematicians, do not always order ligands unambiguously. This problem is particularly noticeable for condensed, aromatic ring systems with a number of atoms different from 6 or other complex and heavily substituted rings with multiple chirality centres.
Algorithms implemented in the software used for registration of chemical structures in databases generate a canonical numbering of atoms independently of the CIP based ordering of ligands. Each atom is uniquely indexed within the structure and the index makes priority ordering of ligands obsolete since the ligands a, b, c, d can be ordered according to their indexes (which after canonicalization are unique). However, canonicalization cannot answer the question if the ligands of a given atom are symmetrical or not. Permuting the indexes of the ligand atoms and registering the structure for various permutations can usually answer this question. If the (alpha)numeric registration string stays constant for all permutation one can assume that the ligands are symmetrical.
Practically all effective canonicalization methods are based on the Morgan algorithm [17]. Internal symmetries within the canonicalized compound lead to a combinatorial explosion which in order to handled from a practical point of view makes the registration algorithm choose some sort of “best” approximation. In effect, it can lead to miss-registered compounds in a database, i.e., the same structure may occur in the database twice or even more times since it carries two or more different registry numbers [18].
The use of the CIP rules ordering ligands during the course of registration is necessary only for structures for which an explicit stereo descriptor or multiple stereo descriptors had to be used in order to identify them. For such cases CIP based descriptors have to be translated into parity attributes which are then directly used in the canonicalization algorithm.
The reverse situation of translating parity into the CIP based descriptors is of no meaning for registration itself, but can be useful for other CT based applications such as for example algorithmically generated nomenclature. This was applied in the AutoNom [19] software package generating systematic nomenclature directly from the connection table of a compound.
Graphical representation of stereochemical information vs. computer representation
Published stereoisomers are graphically depicted using the solid wedge, broken or dashed wedge, broken line, solid bar and open wedge conventions. For special cases Fisher and Newman projection formulas are used. Specialised structure-drawing editors enable entering of complete structures together with the above mentioned graphic representations of stereo characteristics or projection formulas and then translate them into connection tables represented internally as character or binary strings. These strings comply with pre-defined formats. There are great many formats currently in use, usually customised by the owner or the producer of a database. Two formats whose details have been published and which are in widespread use within the chemical community are ROSDAL [20] and MOLFILE [21], both now supported by Molecular Design Limited (MDL). The latter, MOLFILE, has became a quasi standard in computer based chemical information applications.
All formats contain coded information on the atom and bond characteristic of the structure as well as specifications of atom topology in a form of their 2D or 3D coordinates. From a chemical point of view (neglecting here for the time being their role in the structure’s visualisation) the coordinates are only needed for structures with chirality centres and/or geometrical stereochemistry. Unique association of a given asymmetric centre with the correct stereodescriptor, particularly for big, multi-atom structures, is difficult even for an experienced chemist, not to mention the programmer designing a reliable algorithm for computer handling of this task. The difficulties usually derive from the way the structures are drawn on a paper or on the terminal screen. The graphic depiction of structural diagrams is often far from the correct parallel projection of the ideal tetrahedron.
Correct and “clean” graphical representation of stereochemistry in structures, for most of the known computer algorithms handling chirality centres geometry [22] leads, in most of the cases, to correct computer representations, i.e., the algorithm is able to calculate and assign the corresponding, correct, stereodescriptors. The discrepancies come from the differences between the strictly “chemical thinking” and “mathematical thinking” approaches projected into the algorithm. Usually, after detailed analysis, it can be determined that the algorithm had not simulated one-to-one all the operations the chemist executed while assigning stereochemistry to a structure.
Known relevant algorithmic methods of geometrical analysis of stereochemical centres assign some fixed value to the Z-co-ordinate with its sign (direction) determined by the direction of the coded stereo bond (+, positive, for solid bars and solid wedges or -, negative, for broken bars and open wedges). Usually the fixed value is equal to 1 (independent of the co-ordinates scaling) [22], or some “normalised” constant related to the spectrum of X- and Y- coordinates. The crucial weakness of this approach is its ability to also generate results for such cases where manual analysis by a chemist would reject them as absolutely erroneous or inappropriate for analysis. The impact of this weakness can be reduced by introducing additional rules and conventions for coding of stereocentres during data entry of structures [23,24].
Determinant algorithm
In order to eliminate the “fixed Z-coordinate” effect as well as optimise the processing of stereochemical structures during registration in the databases the authors designed and implemented a new effective algorithm for handling of geometry at stereochemical centres. The algorithm, due to its mathematical representation, is described here as the determinant algorithm.
The starting point of the reasoning while designing the algorithm was the obvious assumption that stereoisomers with their variety of spatial distribution of differentiated ligands around an asymmetric centre can be described – mathematically –using the notion of the space orientation (sign of space). For a 3D space, the space orientation is defined by equation (1):

The sign of space is equivalent to the sign of a determinant constructed by unit vectors defining the space itself. It can be easily proved that equation (1) – when traversing from the vector notation to the notation based on four points defining space – can be converted into the fourth grade determinant (2):

The determinant equals zero only for all four points lying on the same plane or for at least two identical points. Relating this equation with the four ligands at stereocentres one can deduce that transformation of configuration can be only achieved for situation when all ligands are located on the same plane. Additionally one can see that in order to create space the points have to be differentiated. Besides, one can see that permutation of two rows of the determinant (2) causes the change of its sign. The determinant (2), when extended at the third column attains the much more practical and convenient representation (3):
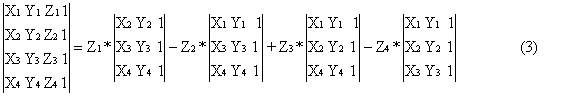
This representation allows one to determine the sign of the determinants (3) [and thus (1) and (2)] without setting any value for the Z-coordinate. For summands having the same sign, the sign of (3) is independent of Z values (Z1, Z2 and Z3) and thus no matter if Z is zero, negative or positive the sign of the sum (3) stays the same. In other words, addition of only positive numbers results in a positive number just as adding only negative numbers leads to a negative result. Besides, the addition of zero to anything does not change the result at all. The conclusion is obvious: if summands with different signs occur in (3), then the structure represented by (3) is unambiguous. It can be proven that the resulting value of (3) depends on particular values of Z and in particular it becomes zero (the case of a flat structure). The determinant (3), when related to a 2D space can be interpreted as 2D space orientation (sign of space) or as the sign of triangle (4):

The determinant (4) is very convenient for manual as well as algorithmic analysis while determining its sign. The manual method (based on graphic representation) is similar to the CIP procedure and consists in moving along sequences of vertexes of the triangle (5). The clockwise direction of the movement corresponds to a negative sign while the counter clockwise one is related to a positive sign of (4).
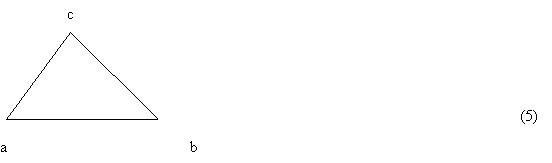
The form (4) of the triangle determinant is not very “computer friendly”. Its grade can however be reduced giving the following form:
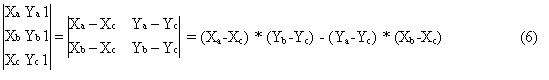
Formula (6) is exceptionally simple to program and can be particularly fast if designed for use with the CPU registers storage technique [18]. It is particularly important for registering very big databases with millions of compounds some of them having multiple stereochemical centres.
Using the determinant algorithm for manual (non algorithmic) assignment of stereochemical centres
If the representation of direct neighbourhood of asymmetric centres in a structure is deformed then usually the stereochemistry of such structures, even during manual assignment by a chemist, is declared as undefined. Direct discussions with nomenclature specialists professionally analysing such structures on an everyday basis for systematic naming purposes [18] before storage in the Beilstein File proved that deformed structure are in most of the cases rejected and declared as “stereochemically ambiguous flat” structures.
It seems that application of equation (3) in the course of the manual stereocentre assignment directly from the graphical representation of a structure is fully possible and should prove to be faster and reliable. In practice it is limited, for a given asymmetric centre, to ranking - using the CIP rules – the ligands a, b ,c, d , selecting the ligand connected to the asymmetric centre with a stereochemical bond and then determining the sign of triangle that can be created by the other ligands. The sign of the triangle is then multiplied by (+1) or (-1) depending on the sign of the chosen Z-coordinate. The sign of the summand in (3) is also considered. Negative values of (3) correspond to the R (rectus) descriptor while a positive one corresponds to S (sinister). The result should be fully independent of the selection of the stereochemical bonding (if more than one such a bonding present). Should selection of different stereochemical bonds lead to different signs of (3), then the asymmetric centre cannot be unambiguously defined. The application of determinant method in the manual stereocentre assignment process can be exemplified using the following real case scenario. The non-steric occurrence of the structure chosen for the example below comes from the Beilstein File where it is registered under the Beilstein Registry Number (BRN): 1900185. Its computer generated (by the AutoNom program) systematic name is 1-aminoethanol. CAS registered this structure under the CAS Registry Number (CRN): 75-39-8
Example:
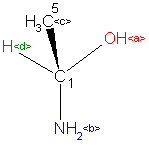
Let us assume the CIP ranking for all ligands at a given stereocentre atom of a structure located ligand c as lying above the plane of the graph. Thus the sign of triangle set by the vertices a, b, and d should be calculated and the route along the vertices a through b and then to d should be analysed. If traversing from a via b to d goes in the clockwise direction then the sign of the third grade determinant is negative. Let us assume for this example that this is the case. Since the c ligand is connected to the asymmetric centre by a steric bond then the sign at the third summand of sum (3) is negative and while ligand c is above the plane then the Z-coordinate is positive. Thus minus multiplied by plus and then once more by minus gives minus and consequently the correct descriptor of the stereocentre is R (rectus).
Stereocentres with only three ligands: case study
It is almost a rule to ignore hydrogen atoms while drawing - and later storing in some supported format – the structural diagrams of compounds. The hydrogen atoms are said to be implicit for such compounds. If the atom with implicit hydrogen(s) is an asymmetric centre (which is a very frequent case) then additional complexity results for models based on the “fixed Z-coordinate”. Assignment of ligands for such centres can be a source of additional errors. The situations get even more complicated if one has to handle three-valent nitrogen whose asymmetry is caused by the pair of electrons.
All these problems have nothing to with our determinant algorithm method at all. The method is not based on pre-determined fixed values of the Z-coordinate, but analyses strictly the signs of the summands in (3). For implicit hydrogen and nitrogen cases it should be assumed that the coordinates of the missing ligand(s) are identical with the central stereocentre atom and the virtual ligand automatically gets the lowest d rank. It can be mathematically proven that such a virtual hydrogen can change the absolute value of the determinant (3) but definitely does not influence the sign of this determinant and thus has meaning in the process of the stereodescriptor assignment.
Stereocentres with four ligands: case study
A central atom with 4 ligands corresponds to 5 points in space while for definition of a 3D space only 4 points are necessary. The additional information can be used for testing the unambiguouity of coding of the stereocentre. For a central atom within an environment of ligands corresponding to a parallel projection of a tetrahedral system the result of the determinant algorithm method is independent of the length of bonds (those drawn in the structural diagram!), However for sketches of stereocentres (and its neighbouring atoms) which correspond to a pyramidal tetrahedron the deformation of the graphic representation can be so extensive that central atom may be determined to be located beyond the walls of the tetrahedron delimited by the ligands. In such cases the structure can be marked as unambiguous or, which should be tried in the first place, the lengths of bonds should be “normalized”.
Geometrical (cis-trans) stereoisomers
Geometrical (or, according to the newest terminology recommendations of IUPAC, cis-trans isomerism) stereoisomers are, by definition, flat objects which makes the algorithmic analysis much easier. The crucial danger, however, while processing geometrical stereoisomers comes from the unavoidable uncertainty whether the asymmetric (if perceived as such) placement of substituents on both sides of the plane set by the unsaturated bond is conscious or simply accidental. Another issue in the case of geometrical stereoisomerism for rings containing unsaturated bonds concerns the size of the smallest ring closures within a ring system. The rings, if supposed to display geometrical isomerism, have to exceed a certain minimum size.
For alkenes the terms cis and trans may be ambiguous, particularly for cases where the main chain in substituted sequences cannot be uniquely determined, and have therefore largely replaced by the E,Z convention. Therefore, according to the latest recommendations of IUPAC for nomenclature of organic compounds the usage of the traditional cis and trans is strongly discouraged [25] and this concerns all classes of compounds and not only alkenes.
The algorithms used in software analysis of geometrical isomers have to assign E,Z descriptors which is a trivial task for mono-substituted atoms connected by a double bond (single non- hydrogen ligand on both sides). In more complex cases of multi-substituted atoms the ligands on one (or both if necessary) atoms of the double bond are ranked using the usual CIP rules and if CIP cannot provide an ultimate unambiguous ranking, the parity attribute and canonical numbering of atoms is used.
Having determined which two ligands attached to atoms that are connected by a double bond are to be compared, one has to find out (calculate) how they are located relative to each other. The double bond is described as E if the two ligands lie on opposite sides of the plane of the double bond, or Z if the ligands are on the same side of the plane. The determinant form that best fits such calculations is given in equation (6). One can easily notice and deduce that the two triangles spread along the double bond edge and with the third vertex at the atom of a ligand have the same sign [according to definition (4)] only if the ligands are on the same side of the double bond plane and different signs if they lie on opposite sides. If the value of (4) is zero or close to zero (it measures the area of the triangle) then the analysed ligand lies co-linearly (or almost co-linearly) with the double bond.
Summary
The determinant algorithm described in this paper was invented, designed, programmed and implemented during the Registry II project launched by the Beilstein Institute in Frankfurt/Main. The purpose of this project was to replace the existing unreliable compound registration software with a better one. Most of the advantages of the new software were expected in the area of stereoisomer registration. The algorithm was (successfully) tested on huge sample of over 3.1 million compounds from the Beilstein File. The data resulting from these tests will be presented and discussed in detail in a future paper.
References and Notes
1. Davis, C.H.; Rush, J.E. Information Retrieval and Documentation in Chemistry; Greenwood Press: London, U.K. 1988, 143.
2. International Union of Pure and Applied Chemistry. Commission on the Nomenclature of Organic Chemistry, Nomenclature of Organic Chemistry, Sections A, B, C, D, E, F and H, 1979 edn, Pergamon Press: Oxford, 1979.
3. Proceedings of the Second International Conference, Noordwijkerhout, The Netherlands, 3-7 June 1990, in Chemical Structures 2. The International Language of Chemistry; Warr, W.A. Ed., Springer-Verlag: Berlin, Heidelberg, 1993.
4. http://www.cas.org/cgi-bin/regreport.pl
5. (a) Molecular Connection, 2000, 19, 26-27; (b) http://www.beilstein.com/beilst_2.shtml
6. Morgan H. J. Chem Doc, 1965, 5, 107-113
7. Wenninger, D.; Weninger , A.; Weninger J.L., J. Chem. Inf. Comput. Sci, 1989, 29, 97-101
8. The 125th Anniversary of the Tetrahedral Carbon Atom Symposium (co-sponsored by the Divisions of Organic Chemistry and History of Chemistry, and the Chemical Heritage Foundation.) at the 218th ACS National Meeting, August 22-26, 1999, New Orleans, Louisiana.
9. Cieplak,T., “The beauty of the graphical structure graph”, in Software Development in Chemistry 5, Gmeling, J. Ed.; Springer-Verlag: Berlin, Heidelberg, 1991, pp. 225-231
10. (a) Moss, G. P. Pure Appl. Chem., 1996, 68, 2193-2222;
(b) http://www.chem.qmw.ac.uk/iupac/stereo/intro.html#gra
(c) Loening K.L., in Chemical Structures.; Warr, W.A., Ed., Springer Verlag: Berlin, Heidelberg,
1988, 413-423.
11. Lin, S-K.; Patiny, L.; Yerin, A.; Wisniewski, J.L.; Testa, B. Enantiomer, 2000, 5, 571-583.
12. Commission on the Nomenclature of Organic Chemistry, IUPAC, Minutes of CNOC Meeting in Frankfurt/Main, Germany, September 2-4, 2000.
13. (a) Cahn, R.S.; Ingold, C.K.; Prelog, V. Angew. Chem. 1966, 78, 413-447 [Angew. Chem. Int. Ed. Eng. 1966, 5, 385-415, 511]; (b) Prelog, V.; Helmchen, G., Angew. Chem. 1982, 94, 614-631 [Angew. Chem. Int.. Ed. Eng. 1982, 21, 567-583; (c) Seebach, D.; Prelog, V., Angew. Chem. 1982, 94, 696-702 [Angew. Chem. Int. Ed. Eng. 1982, 21, 654-660], and citations therein.
14. Mata, P.; Lobo, A.M.; Marshal, C.; Johnson, A.P. Tetrahedron: Asymmetry, 1993, 4, 657-668.
15. Dodziuk, H.; Mirowicz, M. Tetrahedron: Asymmetry, 1990, 1, 171-186.
16. Custer, R.H. Match, 1986, 213-31.
17. Morgan, H. J. Chem Doc, 1965, 5, 107-113.
18. Cieplak, T., Beilstein Institut, REGISTRY II, Internal Communication, 1992.
19. Wisniewski J.L.: “Nomenclature: Automatic Generation and Conversion”. In Encyclopedia of Computational Chemistry, P. von Rague Schleyer (Editor-in-Chief), N.L. Allinger, T. Clark, J. Gesteiger, P.A. Kollman, H. F. Schaefer III, P.R. Schreiner (Eds.), John Wiley & Sons Ltd.: Chichester, U.K. 1998, Volume 3.
20. Rohbeck, H.G., “Representation of Structure Description Arranged Lineary”, in Software Development in Chemistry 5, Gmeling, J. Ed.; Springer-Verlag: Berlin, Heidelberg, 1991, pp. 49-58
21. Dalby, A.; Nourse, J.G.; Hounshell, W.D.; Gushurst, A.K.I.; Grier, D.L.; Leland, B.A.; Laufer, J. J. Chem. Inf. Comp. Sci., 1992, 32, 244-255.
22. Rohde, B., “Represenation and Manipulation of Stereochemistry“, in Encyclopedia of Computational Chemistry, P. von Rague Schleyer (Editor-in-Chief), N.L. Allinger; T. Clark; J. Gesteiger; P.A. Kollman; H. F. Schaefer III; P.R. Schreiner (Eds.), John Wiley & Sons Ltd.: Chichester, U.K. 1998, Volume 3.
23. Polton, D.J. Online Review, 1982, 6, 235-242.
24. Staggenborg, L.M.: “Stereochemistry in the CAS Registry File Chemical Abstracts Service”, in Recent Advances in Chemical Information, Colier, H. Ed., Royal Society of Chemistry: Cambridge, U.K. 1993, 89-112.
25. Basic Terminology of Stereochemistry, Draft 8, (November 1992), Joint Working Party on Stereochemical Terminology, IUPAC (Draft available from the authors)
Sample Availability: Not applicable