Organic Chemistry Laboratory,
Swiss Federal Institute of Technology, ETH-Zentrum, CH-8092 Zürich,
Switzerland
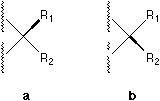
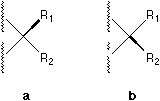
ABSTRACT The broken wedge, broken line, solid bar, and
broken bar are either not reasonable or can be replaced by only one type
of solid wedge in the stereochemical formulation. A convention based on
a one-wedge symbolization is proposed, where a or b is used
instead of c, d, e, f, g, or h.

INTRODUCTION
Human-beings and molecules alike exist in a three-dimensional physical world. But so far our custom is to record information on paper which is a two-dimensional medium. A three-dimensional configuration1 can be described by a set of coordinates (xi, yi, zi) which can be listed on paper, or by three projections on the XY, YZ, XZ planes as three figures. These presentations, though scientifically accurate, are not convenient. Instead of three projections, normally a single perspective drawing is used, which is comfortable to understand and sometimes can be accurate and non-confusing also. Sometimes a convention should be adopted and obeyed. In organic chemistry, for tetrahedral centers, Newman projection and Fischer projection are conventions used conveniently for certain purposes such as conformational analysis and for certain categories of compounds such as saccharides. A more generally and trivially used convention is to indicate the position of a ligand (a group, electron pair etc.) above the plane of the paper by a solid wedge and ligand below the paper plane by a broken line,2,3 see 1.
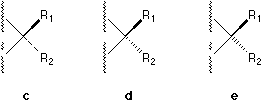
Besides solid wedge and broken line, there are also broken wedges used by many authors which are either against perspective principle (See 2, but it is interesting and strange that most people, including the present author, feel that 2 looks more comfortable than 3!) or unnecessary (See 3), as correctly commented by Testa.4
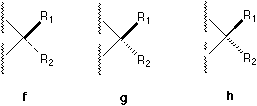
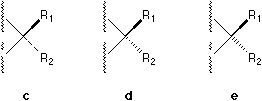
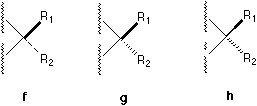
In ChemDrawTM there are five different available notations (see Figure 1) and a large number of their combinations which can be found in literature. For example, a solid bar5 and a broken bar6 are constantly used by famous organic chemists like Heathcock in their textbooks and publications.
As indicated by Testa,4 confusion may be difficult
to avoid if so many ways of presentation coexist in chemical literature.
Therefore, there is strong reason to discuss this problem, try to set up
a reasonable convention, and convince the chemical community to systematically
follow the convention. It is the purpose of this paper to propose a convention
based on a single solid wedge formulation of molecular systems containing
tetrahedral centers.
ONE SOLID WEDGE IS ENOUGH
In a stereochemical formula, factually a broken line, a broken wedge, or a broken bar, which are used to indicate a bond pointing behind the plane of the paper, can be replaced by a solid wedge pointing from the chiral center to the ligand (see the group R2 in 4) if their involvement is necessary. Actually it is always possible to employ a single solid wedge in the perspective indication of the absolute configuration of a center. It is virtually not necessary to use other type of marks.
The use of a solid bar or a broken bar should be banned, because it brings forth confusion when there are two chiral centers involved at the two ends of the bond if complicated molecular formula is encountered. As strongly argued by Testa, the use of broken wedges should also be banned.4 On the other hand, the notations of broken lines must be reserved to indicate relatively weak interactions or H-bonding or van der Waals interactions.
A solid wedge has two functions: representing a single bond which defines a straight line, and indicating the orientation of the bond. It is also clear that three points (or three ligands here) can define a triangle which can represent a two-dimensional plane. It is perspectively conceivable that when a wedge is connected to a chiral center located on the paper, the the triangle and the three pyramidal bonds attached to the center will push the wedge out of the plane of the paper. For example, in 5, group R4 is above the paper, as a consequence that the three groups R1, R2, and R3 and the triangle connecting them behind the paper plane push R4 out of the plane of the paper.
In a four-center configuration, with the center C outside of the
triangle plane, the order of the three groups (R1, R2,
and R3) and the corresponding three bonds in the pyramidal C-R1-R2-R3
is well defined and can be found out by inspection without difficulty.
This perspective is illustrated by 7
and 8, which correspond
to 5 and 6 respectively. Suppose R1 > R2
> R3 > R4 and follow the CIP convention.7,8
Then, the absolute configurations of 5 and 6 are S
and R respectively. In conclusion, we find out that only one type
of bond mark, a solid wedge, is enough for stereochemical formula description
of configuration, and only one such wedge is needed for the unambiguous
specification per quadrivalent chiral center.
THE CONVENTION
Based on these arguments, we propose the following convention for quadrivalent chiral center which is well-defined and may be intuitively easy to follow.
I. One and only one solid wedge is used per center.
II. Only the chiral center concerned is at the plane of the paper. The ligand bearing the solid wedge and the triangle composing the rest three groups, are always at the two opposite sides of the paper.
III. When the wedge points from the ligand to the center, the ligand bearing the solid wedge is above the paper. When the wedge points from the center to the ligand, the ligand bearing the solid wedge is below the paper.
IV. The place of the ligand bearing the solid wedge has no influence of the configurations. The form of the triangle defined by the rest three ligands has no influence of the configurations, but the sense counting along the pericycle of the triangle is important.
V. When only three bonds are drawn, the missing ligand can be an electron pair or a hydrogen, and is eclipsed with the ligand bearing the solid wedge.
Item I is self-evident. Item II means that in this convention only the chiral center is situated on the paper. This is different from the conventions used currently where two ligands and the center are thought on the paper plane (See 1, 2, 3, and 4) and the rest two ligands and the center are on a plane perpendicular to the former. Item III is illustrated by 5 and 6. There are three parallel planes in the formula convention here: The first plane, the plane of the paper, contains the center. The second plane contains the ligands with normal bond symbols. And the third plane, which is on the opposite side of the paper, contains the ligand with solid wedge. If we follow this three-plane system, we may use the present 'one-wedge convention' to specify the absolute configuration of penta- and hexa-coordinated compounds where one type of solid wedge is used, but the number of solid wedges used can be more than one. Our present discussion is concentrated on systems with quadrivalent centers where only one type of solid wedges is used and the number of solid wedge used is always one.
In order to exemplify item IV, we recognize that 9, 10, 11 and 12 are all of the same absolute configuration as 5. In 9, the ligand bearing the solid wedge is in between R2 and R3, while in 10, the ligand is in between R1 and R2. That means the place of the ligand bearing the solid wedge has no influence of the configurations. In 11 and 12, the positions of R1, R2 and R3 in their corresponding triangles are different. In 12, the three groups R1, R2 and R3 are more close together but still define clearly a triangle, which indicate the same order of R1 to R2 to R3 to R1 as the triangles defined in 5, 9, 10 and 11. Their arrangements are all the form as shown in 13 or 7. However, in comparing 11 and 14, the order of R1, R2 and R3 in their corresponding triangles (13 and 15) in the two molecules are different. The molecule 14 is in fact the same as 6. The form of the triangle, whether it is equilateral, isosceles or not, defined by the rest three ligands, has no influence on the configuration. Only the sense counting along the pericycle of the triangle is important.
This flexibility is very useful when drawing a formula with a chiral center at a crowded site in a complicated molecule. In contrast, the tetrahedral chiral center was always drawn as a rigid cross in Fischer convention, and such flexibility may not be available. By following the present convention, it also seems easier to inspect a chiral center and specify stereoisomers by the CIP system.
It should keep in mind when one visualizes the form of the triangle that the three pyramidal bonds attached to the center are in principle of the same length (Figure 2).
Item V is listed to conform the conventional simplification. There is a popular custom of omitting hydrogen (see the alcohol 16 or 18) or lone electron pair in a tetrahedral sp3 hybridized center (see the sulfoxide 17 or 19) when drawing formula.6,9 In 16 or 17, the missing ligands are hidden below the paper behind the OH or O- groups. In 18 or 19, the missing ligands are above the paper and in front of OH or O- groups.
Incidentally, it is known that there are three ways of drawing sulfoxide4 SO bond and there are two ways of drawing NO bond in N-oxides, see Figure 3. If the NO or SO bond is used to specify absolute configuration as a solid wedge, a single bond bearing positive charge on the center (S or N) and a negative charge on O should be adopted, see Figure 3a and 3d. Otherwise all these five forms are legal.
When no wedge is used, naturally, this implies that the absolute configuration
of the chiral center is not specified.
CHAINS AND CYCLES
The examples given above are all have only one isolated chiral center. The present convention can however be applied to more complicated cases. Factually the merit of this convention relies on its feasibility to a chain system composed of several chiral centers, a cyclic system of several chiral centers or more complicated cases of network.
The Fischer projection of D-glucose 20 can be rearranged and easily and concisely represented with only two wedges, see 21. Surely the formula in 21 or 22 are more realistic than 20. All these molecules (20, 21, and 22) are of the same absolute configuration.
Generally speaking, for a chain system of n chiral centers, the structure can be arranged in such an optimistic way that only n/2 wedges are needed if n is even, or (n+1)/2 wedges if n is odd.
Similarly, for a cyclic system of n chiral centers here, only n/2 wedges are needed if n is even, or (n+1)/2 wedges are needed if n is odd. For example, the three membered ring 23 and the five membered ring 24 need 2 and 3 wedges respectively to exactly indicate their absolute configurations. The Fischer projection of cyclic molecule is difficult or not reasonable. The present convention may be easily used to more complicated cases also.
Due to historical reason, one can be well-justified to use the Fischer
convention for carbon chain molecules such as D-glucose 20. Minimum
number of wedges were used in 21 to 24. But obviously one
can feel free to use more wedges instead of the number of wedges connecting
chiral centers. That means four wedges can be applied to the usual formula
20,
where one wedge per chiral center will be used, and that still conforms
the recommendation of the one-wedge convention.
CONCLUSION
The above discussions argue that broken wedge, broken line, solid bar, and broken bar are either not reasonable or can be replaced by only one type of solid wedge. We proposed a simple and unequivocal method for uniform stereochemical drawing of formulae. A convention based on this one wedge symbolization has been developed where a or b is used instead of c, d, e, f, g, or h.
Possibly the present convention also is helpful to computer-assisted indexing and literature search of certain chiral molecules.
ACKNOWLEDGMENTS
The author thanks Professors Bernard Testa (University of Lausanne) and Miklos Simonyi (Hungarian Academy of Science) for their encouragement. He also thanks Professor Dieter Seebach (ETH-Zentrum) for his stimulating lectures of organic synthesis and for his generous supply of reprints of book-size review article.
LITERATURE CITED
1. Maxwell, J.C. Matter and Motion, Notes and Appendices by J. Larmor. New York: Dover, 1952.
2. Hendrickson, J.B., Cram, D.J., Hammond, G.S. Organic chemistry. 3rd ed., New York: McGraw-Hill, 1970.
3. Testa, B. Principles of organic stereochemistry. New York: Dekker, 1979.
4. Testa, B. On flying wedges, crashing wedges, and perspective-blind stereochemists. Chirality, 3:159-160, 1991.
5. Streitwieser, A. Jr., Heathcock, C.H. Introduction to organic chemistry. 3rd ed., New York: Macmillan, 1985.
6. Heathcock, C.H. Understanding and controlling diastereofacial selectivity in carbon-carbon bond-forming reactions. Aldrichimica Acta, 23:99-111, 1990.
7. Cahn, R.S., Ingold, C.K., Prelog, V. Spezifikation der molekularen Chiralität, 78:413-447, 1966; Cahn, R. S., Ingold, C.K., Prelog, V. Specification of molecular chirality. Angew. Chem. Int. Ed. Engl. 5:385-415, 1966.
8. Prelog, V. My 132 semesters of chemistry studies. Washington, D.C: American Chemical Society, 1991:74.
9. Seebach, D. Organische Synthese--wohin? Angew. Chem. 102:1363-1409,
1990; Seebach, D. Organic synthesis--where next? Angew. Chem. Int. Ed.
Engl. 29:1320-1367, 1990.
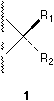
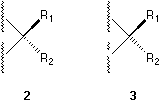
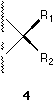
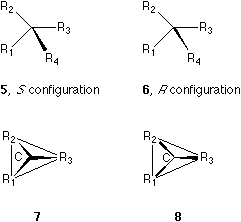
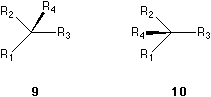
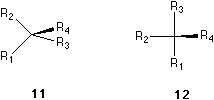
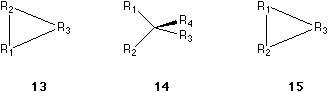
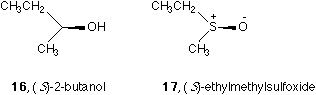
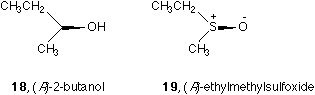
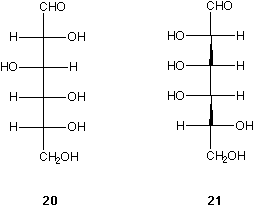
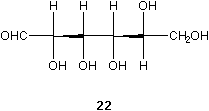
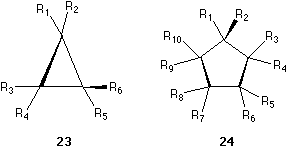
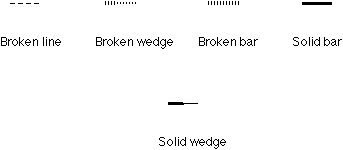
Fig. 1. Various bonds used to perspective specification.
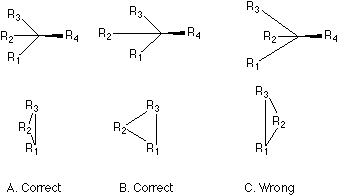
Fig. 2 The way of drawing the three bonds in formula C may be allowed, but we should visualize the form of the triangle in a way that the three pyramidal bonds attached to the center are of the same length (formula A). When the three pyramidal bonds or the three groups are too crowded (formula A), it will be helpful to stretch the central bond (here the bond bearing R2 in formula B) of the three bonds during the visualization.
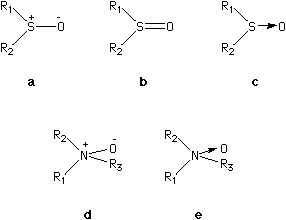
Fig. 3. Different legal formulas for sulfoxides and N-oxides