3 EFFECTS OF THE RELATIVE VALUE OF RATE CONSTANTS ON THE KINETIC CURVES
The kinetic equations of successive reactions are defined by two rate constants k₁ and k₂, but the overall reaction is not a simple mathematical addition of two simple reactions. The contribution of two simple reactions to the successive reaction is decided by the relative value of k₁ and k₂. Let r = k₂/k₁, then the kinetic equation of B, C, R will be:

[B]_t = [A]₀ (e ^- e) /(r-1)                                                             (17)

[C]_t = [A]₀ [1 - (r e ^- e)/(r-1)]                                                   (18)

[R]_t = [A]₀ [(m + n)(r - 1) + ( m - (m + n) r)e + n e]/(r-1)                           (19)

    As can be seen, the coefficients of powered term are defined only by r, and have no relationship with the absolute value of k₁ and k₂. In order to study the effects of r on the kinetic curves of successive reaction, we simulated a series of kinetic curves of concentration and rate at different r value. The r value is changed by fixing k₁ and changing the value of k₂.



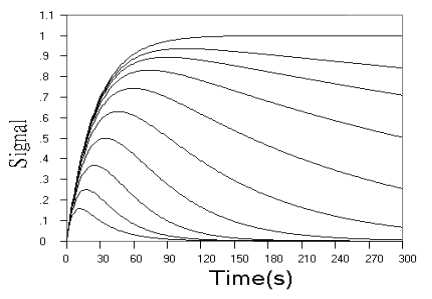
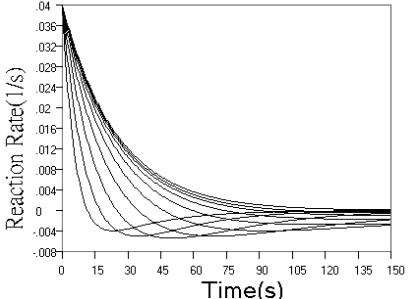
Fig.1 Simulated concentration (upper panel) and rate (lower panel) curves based on detecting intermediate product in successive reactions. In each panel from ground to top, k₁ = 0.04 s^-1, k₂ = 0.16, 0.08, 0.04, 0.02, 0.01, 0.005, 0.0025, 0.00125, 0.000625, 0 s^-1 respectively.

    Fig.1 shows the kinetic curves of concentration and rate for detection of the intermediate product in successive reaction. As can be seen from the concentration curves in Fig.1, the maximum concentration of intermediate product decreased, and the time need to reach the maximum reduced, when r value increased. When r value decreased, the starting phase of the kinetic curve overlapped more and more, and the maximum concentration of intermediate product approached the initial concentration of analyte more and more closely, and the time need to reach the maximum approached the end point of the first step reaction more and more closely. The rate curves of Fig.1 reflect these changes more sensitively. When r increased, the reaction rate in starting phase decreased to a minimum almost linearly with time, and when r decreased, the overlapped part of the rate curve in starting phase increased more and more, indicating that the effect of k₂ on the reaction is smaller and smaller.


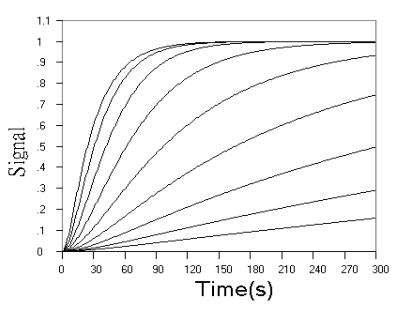
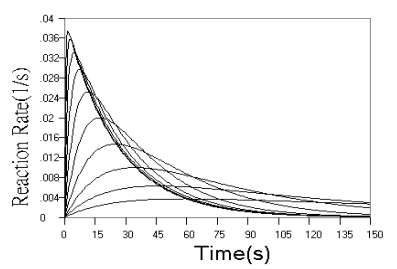
Fig.2 Simulated concentration (upper panel) and rate (lower panel) curves based on detecting final product in successive reactions. In upper panel from top to ground, k₁ = 0.04 s^-1, k₂ = 0.16, 0.08, 0.04, 0.02, 0.01, 0.005, 0.0025, 0.00125, 0.000625, 0 s^-1 respectively. In lower panel from top to ground, k₁ = 0.04 s^-1, k₂ = 2.56, 1.28, 0.64, 0.32, 0.16, 0.08, 0.04, 0.02, 0.01, 0.005 s^-1 respectively.

    Fig.2 shows the concentration and rate kinetic curves for detection of the final product in successive reactions. When r value increased, the difference between kinetic curves turned to be smaller and smaller, and approached a limit of the simple first step reaction kinetics, as can be seen from the concentration curves in Fig.2 and further confirmed by the rate curves in Fig.2. From rate curves in Fig.2, the changes in the starting phase of the kinetic curves can be seen more clearly. When r value decreased, the overall reaction turned to be determined by the second step reaction, When r increased, the reaction rate increased from zero to a maximum almost linearly with time.
    Fig.3 shows the concentration and rate kinetic curves for detection of the reagent in successive reactions. As can be seen from the concentration curves in Fig.3, when r value increased, the kinetic curves turned to approach a limit of the simple first step reaction kinetics, but the sensitivity is doubled, When r value decreased, the starting phase of the kinetic curve turned to be overlapped with simple first step reaction, and the terminal phase of the reaction is almost determined by second step reaction. These observations are further confirmed more clearly by rate curves in Fig.3. Another finding from rate curves in Fig.3 is that when r increased above a value, the rate maximum occurs and approaches the limit of (m + n)[A₀] k_1.


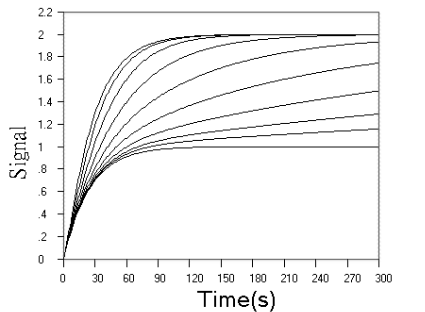
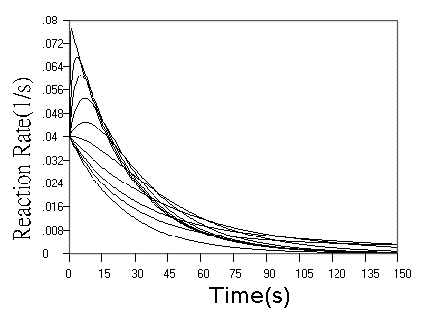
Fig.3 Simulated concentration (upper panel) and rate (lower panel) curves based on detecting reagent in successive reactions. In the two panel, m = n = 1, k₁ = 0.04 s^-1. In upper panel from top to ground, k₂ = 0.16, 0.08, 0.04, 0.02, 0.01, 0.005, 0.0025, 0.00125, 0.000625, 0 s^-1 respectively. In lower panel from top to ground, k₂ = 5.12, 0.64, 0.32, 0.16, 0.08, 0.04, 0.02, 0.01, 0.005,0 s^-1 respectively.

     Some important results obtained by simulation studies and theoretical analyses are summarized in Table2. These results can offer guidelines for us to control a proper r value to increase the kinetic difference between analytes, and help us evaluate the exploitation value of successive reactions in analytical chemistry. When nonlinear least square method was applied to obtain concentrations and rate constants, good initial estimates of these parameters can be obtained by disposal of approximated kinetic equations in Table2. From simulation studies, we can learn that the overall kinetic behaviour is determined by r value only. Only a limited range, approximately from 1/16 to 16, is allowed for r value to maintain the real successive reactions. We can exloit this property to enlarge the kinetic difference between analytes by control the r value.

Table2 Effects of relative value of rate constants on successive reactions

Curve	r value	Effects
B	r → ∞ ( r > 20)	Impossible to detect B
	r → 0 (r< 1/8 )	1. Starting phase approximated as [B]t = [A]0(1- e) 2. Terminal phase approximated as [B]t = [A]0 e
	Middle	1.Starting phase approximated as [B]t = [A]0k1(t- (k1 + k2)t2/2) 2. Terminal phase approximated as [B]t = [A]0 e/(r-1) when k2 > k1, or [B]t = [A]0 e/(r-1) when k2 < k1
C	r → ∞ ( r > 8)	Kinetic curve approximated as [C]t = [A]0(1- e)
	r → 0 (r<1/16)	Kinetic curve approximated as [C]t = [A]0(1- e)
	Middle	1. Starting phase approximated as [C]t =  [A]0k1k2t2/2 2. Terminal phase approximated as [C]t = [A]0 (1- r e/(r-1)) when k2 > k1, or [C]t = [A]0 (1- e) when k2 < k1
R	r → ∞ ( r > 8)	Kinetic curve approximated as [R]t = (m + n)[A]0(1- e)
	r → 0 (r< 1/8 )	1.Starting phase approximated as [R]t = m [A]0(1- e) 2.Terminal phase approximated as [R]t = [A]0 ((m + n)-n e)
	Middle	1. Starting phase approximated as [R]t = [A]0k1 {m t +  ( m k1 – ( m + n) k2 + n k2) t2/[2(r-1)]} 2. Terminal phase approximated as [R]t = [A]0 ((m + n) + e(m-(m+n)r)/(r-1)) when k2 > k1, or [R]t = [A]0 ((m + n) + n e/(r-1)) when k2 < k1

4 THE SITUATIONS MAY BE ENCOUNTERED IN KINETIC ANALYSIS BASED ON SUCCESSIVE REACTIONS
According to the effects of r value on the kinetic curves of successive reactions, we can propose various situations that may be encountered in real analysis. It is nessary to evaluate which situation is favourable to analysis and what is unfavourable, as it can guide us select proper experiment conditions to control the right r value, and perform selective or simultaneous determinations.
    Consider binary mixtures of A and A', the rate constants in successive reactions of A and A' are k₁, k₂ and k₁' and k₂' respectively. Nine situations may be encountered in real analysis and they are summarized in Table3. The most unfavourable situation is No.1, because it is impossible to detect B, and the exploitable rate constants for detecting C and R is only k₁ and k₁', k₂ and k₂' lose its present value. In this situation, the successive reaction of C and R is in fact degenerated to simple reaction. The unfavourable situation is No.4, the successive reaction for detecting B and R degenerated to two separated simple reactions, for detecting C, it degenerated to simple reaction. The less favourable situation is No.9, the r value remains in successive region for both analytes. The most favourable situation is that, one analyte has a r value remain in the successive reaction region, while another analyte has a r value out of the range, such as No.2,3,5,6,7,8 etc.. In these situations, the kinetic difference between two analytes can be enlarged due to the presence of the second step reaction in the successive reactions.

Table3 Situations may be encountered in kinetic analysis based on successive reactions