http://www.chemistrymag.org/cji/2005/07a068pe.htm |
Oct. 12, 2005 Vol.7 No.10 P.68 Copyright |
Dong Yanhui, Chen Yao
(Department of Chemistry, Jinan University, Guangzhou, 510632)
Received on Aug. 8, 2005; Supported by Foundation of Ministry of Education (No.2002247), Foundation of Jinan University (No.640071) and Foundation of Guangdong province (No.2003C33101).
Abstract Liquid–liqud equilibrium tie line data were determined for the quaternary
system of water + 2-propanol + methyl tert-butyl ether + toluene at 298.15 K and
ambient pressure. The experimental liquid–liquid
equilibrium results have been successfully correlated by modified and extended UNIQUAC
models both with ternary and quaternary parameters in addition to binary ones.
Keywords Liquid–liquid equilibria, Oxygenated
compounds, Quaternary mixtures, Modified and extended UNIQUAC models
1. INTRODUCTION
Reformulated gasoline includes certain oxygenated compounds such as
alcohols and ethers. These are commonly methanol, ethanol, propanols, and butanols as well
as methyl tert-butyl ether (MTBE), ethyl tert-butyl ether (ETBE), and tert-amyl
methyl ether (TAME). These oxygenated compounds are added to improve the octane rating and
pollution-reducing capability of gasoline. MTBE is the primary oxygenated compound
currently used in reformulated gasoline because of its low Reid vapor pressure (RVP) and
the availability of the feedstock ethanol from renewable resources. In this sense, there
has been an increasing interest in the thermodynamic behavior of liquid mixtures of MTBE
with gasoline-substitution hydrocarbons. The multicomponent phase equilibria of the
oxygenate ether and alcohol mixtures with water are useful and considerably focused not
only on the process design for reformulated gasoline production but also on the problem of
contamination of groundwater. Here we report liquid–liquid equilibrium (LLE) measurements
on one quaternary system water + 2-propanol + MTBE + toluene at 298.15 K. The experimental
LLE data were correlated by means of the modified UNIQUAC and extended UNIQUAC models
[1,2] including both ternary and quaternary parameters coming from
multicomponent intermolecular interactions, in addition to binary parameters. The
constituent ternary systems of water + 2-propanol + toluene [3], water + 2-propanol + MTBE, water + MTBE + toluene [4], were used to obtain ternary parameters for accurate representation of the
quaternary LLE system studied in this work. The binary parameters of miscible binary
mixtures of constituents of the ternary and quaternary systems were obtained from vapor–liquid equilibrium data [5-8] and those of immiscible mixtures were obtained from mutual solubility
data [9,10].
2. EXPERIMENTS
2.1 Materials
MTBE was purchased from Tedia Company, Inc. with nominal minimum mass fraction of
99.8%. Toluene was supplied by the Guangzhou Chemical Reagent Factory with minimum mass
fraction of 99.5%. 2-propanol was obtained from the Tianjin Chemical Reagent Institute
with nominal minimum mass fractions 99.7%. All chemicals were used without further
purification. GC analysis did not detect appreciable peaks. Water was distilled twice.
2.2 Apparatus and Procedures
Quaternary LLE measurements were carried out at (298.15±0.01)K. The experimental
apparatus and procedure were described previously [11]. About 70 mL of
each quaternary mixture was stirred by a magnetic stirrer for 3 hours and allowed to
settle for 3 hours, which was sufficient for separation into two phases. The samples
withdrawn from upper and lower phases were analyzed by a gas chromatography (Shanghai
Analytical Apparatus Factory, GC-122). The accuracy of the measurements was estimated
within ±0.001 in mole fraction.
2.3 Experimental results
Table 1 shows experimental LLE data for the water + 2-propanol + MTBE + toluene mixtures.
Table 1 Equilibrium phase compositions
in mole fraction ![]() for the quaternary mixtures of water (1)
+ 2-propanol (2) + MTBE (3) + toluene (4) at 298.15 K
for the quaternary mixtures of water (1)
+ 2-propanol (2) + MTBE (3) + toluene (4) at 298.15 K
Organic phase |
Aqueous phase |
||||
|
|
|
|
|
|
{ |
|||||
0.0165 |
0.0252 |
0.2235 |
0.9776 |
0.0205 |
0.0019 |
0.0247 |
0.0486 |
0.2186 |
0.9667 |
0.0305 |
0.0024 |
0.0567 |
0.1253 |
0.1992 |
0.9467 |
0.0506 |
0.0022 |
0.0860 |
0.2084 |
0.1775 |
0.9351 |
0.0612 |
0.0029 |
0.1376 |
0.2710 |
0.1505 |
0.9217 |
0.0735 |
0.0037 |
0.1907 |
0.3089 |
0.1198 |
0.9125 |
0.0810 |
0.0046 |
0.2395 |
0.3426 |
0.0988 |
0.8976 |
0.0935 |
0.0053 |
0.3047 |
0.3551 |
0.0796 |
0.8842 |
0.1059 |
0.0058 |
0.3459 |
0.3635 |
0.0721 |
0.8773 |
0.1114 |
0.0065 |
0.4232 |
0.3728 |
0.0369 |
0.8582 |
0.1286 |
0.0073 |
0.0264 |
0.0289 |
0.4629 |
0.9803 |
0.0152 |
0.0045 |
0.0393 |
0.0699 |
0.4330 |
0.9670 |
0.0280 |
0.0050 |
0.0797 |
0.1474 |
0.3754 |
0.9497 |
0.0442 |
0.0058 |
0.1489 |
0.1951 |
0.3133 |
0.9363 |
0.0568 |
0.0065 |
0.2057 |
0.2836 |
0.2507 |
0.9256 |
0.0668 |
0.0069 |
0.2857 |
0.3156 |
0.1964 |
0.9196 |
0.0722 |
0.0073 |
0.3316 |
0.3304 |
0.1638 |
0.9097 |
0.0813 |
0.0077 |
0.3855 |
0.3416 |
0.1395 |
0.8993 |
0.0907 |
0.0081 |
0.4405 |
0.3361 |
0.1121 |
0.8877 |
0.1011 |
0.0087 |
0.0556 |
0.0431 |
0.6602 |
0.9789 |
0.0153 |
0.0058 |
0.0744 |
0.0818 |
0.6153 |
0.9666 |
0.0274 |
0.0060 |
0.1378 |
0.1725 |
0.5055 |
0.9537 |
0.0398 |
0.0065 |
0.2154 |
0.2255 |
0.4068 |
0.9437 |
0.0495 |
0.0068 |
0.2890 |
0.2707 |
0.3270 |
0.9350 |
0.0579 |
0.0071 |
0.3572 |
0.2868 |
0.2670 |
0.9231 |
0.0685 |
0.0078 |
0.4437 |
0.2970 |
0.1882 |
0.9146 |
0.0773 |
0.0075 |
3. CALCULATION PROCEDURE AND RESULTS
3.1 Calculation procedure
We have used the modified UNIQUAC[1] and extended UNIQUAC[2] models with binary and additional ternary and quaternary
parameters for an accurate description of the experimental quaternary LLE data and
constituent ternary data as well as binary VLE and mutual solubility data.
The binary parameter ![]() defined by the binary energy parameter aji is expressed as
defined by the binary energy parameter aji is expressed as
![]() (1)
(1)
where aji can be obtained from binary experimental
phase equilibrium data, and C was set to 1 for the extended UNIQUAC and 0.65 for
the modified UNIQUAC.
The binary energy parameters for the miscible mixtures were obtained
from the VLE data reduction using the following thermodynamic equations[12]:
![]() (2)
(2)
![]() (3)
(3)
where P, x, y, and g are the total
pressure, the liquid-phase mole fraction, the vapor-phase mole fraction, and the activity
coefficient, respectively. The pure component vapor pressure, ![]() , was calculated by using the Antoine equation
with coefficients taken from the literatures[13,14]. The liquid molar volume,
, was calculated by using the Antoine equation
with coefficients taken from the literatures[13,14]. The liquid molar volume, ![]() , was
obtained by a modified Rackett equation[15]. The fugacity
coefficient, F,
was calculated by the Eqn.(3). The pure and cross second virial coefficients, B, were
estimated by the method of Hayden and O' Connell[16]. The binary energy parameters for the partially miscible mixtures
were obtained by solving the following thermodynamic equations simultaneously.
, was
obtained by a modified Rackett equation[15]. The fugacity
coefficient, F,
was calculated by the Eqn.(3). The pure and cross second virial coefficients, B, were
estimated by the method of Hayden and O' Connell[16]. The binary energy parameters for the partially miscible mixtures
were obtained by solving the following thermodynamic equations simultaneously.
![]() (4)
(4)
![]() and
and ![]() ( I, II = two liquid phases )
(5)
( I, II = two liquid phases )
(5)
The ternary and quaternary LLE calculations were carried out using the
Eqns.(4) and (5). For the ternary systems of type 1 having a plait point, two-parameter
UNIQUAC models predict generally larger solubility envelope than the experimental one. It
is necessary to correlate ternary and quaternary LLE using ternary and quaternary
parameters in addition to binary ones. The additional ternary parameter tijk was obtained by
fitting the model to the ternary experimental LLE data and the quaternary parameter
F =
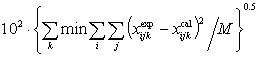 (6)
(6)where min means minimum values, i = 1 to 3 for ternary mixtures or i =1 to 4 for quaternary mixtures, j = phases I and II, k = 1,2,…,n (no. of tie lines), M = 2ni, and x = (the liquid-phase mole fraction).
3.2 Calculation results
Table 2 presents the constituent binary energy parameters of the modified and extended
UNIQUAC models.Table 3 shows the ternary parameters obtained in fitting the modified and
extended UNIQUAC models to the experimental ternary LLE systems, and root-mean-square
deviation of the mole fraction of tie lines between the experimental and calculated
results for the ternary LLE systems. It seems that the modified UNIQUAC model with the
only binary parameters predicts the ternary LLEs more successfully than the extended
UNIQUAC model, and these models can give a much more accurate representation for the
ternary LLEs by including the ternary parameters in addition to the binary ones. Figure 1
compares the experimental and correlated liquid–liquid
equilibrium results of three boundary ternary systems making up the quaternary system at T
= 298.15 K. Good agreement between the experimental values and those correlated using
additional ternary parameters shows in the figure. The quaternary system exhibits type 2
quaternary liquid–liquid behavior[18],
which are composed of two ternary liquid–liquid
equilibium for the mixtures (water + 2-propanol + MTBE) and (water + 2-propanol + toluene)
classified as type 1, and one ternary liquid–liquid
equilibrium for the mixtures (water + MTBE + toluene) as type 2.
Table 4 summarizes the quaternary LLE results predicted by the modified
UNIQUAC and extended UNIQUAC models with the binary and ternary parameters, together with
those correlated with binary, ternary, and quaternary parameters. The root-mean-squared
deviations predicted using the binary and ternary parameters are slightly large for the
water + 2-propanol + MTBE + toluene system, but both models can describe accurately the
quaternary experimental LLE data by the correlation involving the additional quaternary
parameters, and the correlated RMS is 0.94 mol% for the modified UNIQUAC model and 1.80
mol% for the extended UNIQUAC model.
Table 2 Calculated results of binary phase equilibrium data reduction
System (1+2) |
T /K |
No. of data points |
Model |
Energy parameters |
Ref. |
|
a12/K |
a21/K |
|||||
2-Propanol+water |
303.15 |
16 |
Ia |
330.21 308.89 |
–44.88 |
[5] |
2-Propanol+toluene |
298.15 |
13 |
I |
67.90 |
812.97 |
[6] |
2-Propanol +MTBE |
308.24 |
17 |
I |
–44.58 |
480.78 |
[7] |
MTBE + toluene |
333.15 |
10 |
I |
–222.93 |
334.43 |
[8] |
MTBE + water |
298.15 |
MSc |
I |
1196.10 |
173.24 |
[9] |
Toluene + water |
298.15 |
MS |
I |
1713.30 |
752.99 |
[10] |
a
Modified UNIQUAC model; bExtended UNIQUAC model; cMutual solubilities.Table 3 Calculated results for ternary liquid-liquid equilibrium at 298.15 K
System (1+2+3) |
No. of tie lines |
Model |
Ternary parameters |
RMSc |
Ref. |
|||
t231 |
t132 | t123 | ||||||
| Water + 2-propanol + toluene | 12 |
Ia |
–0.1818 |
0.4273 |
0.5157 |
3.46d |
1.45e |
[3] |
| Water + 2-propanol + MTBE | 11 |
I |
–0.2321 |
0.0542 |
1.4993 |
3.42 |
0.53 |
|
Water + MTBE +toluene |
13 |
I |
0.0033 |
0.0133 |
0.0127 |
0.17 |
0.13 |
[4] |
a
Modified UNIQUAC model; b Extended UNIQUAC model; c Root-mean-square deviation[mol%];d Predicted with binary parameters alone; eCorrelated with binary and ternary parameters.
Table 4 Calculated results for quaternary liquid-liquid equilibrium at 298.15 K
System(1+2+3+4) |
No. of tie lines |
Model |
Quaternary parameters |
RMSc |
||||
| t2341 | t1342 | t1243 | t1234 | |||||
Water + 2-propanol |
26 |
Ia |
–0.8919 |
–0.5252 |
1.1752 |
0.8200 |
1.04d |
0.94e |
IIb |
8.1515 |
–15.2339 |
34.4396 |
3.1539 |
3.09 |
1.80 |
||
a
Modified UNIQUAC model; b Extended UNIQUAC model; c Root-mean-square deviation[mol%];d Predicted with only binary parameters; eCorrelated with binary ,ternary and quaternary parameters.
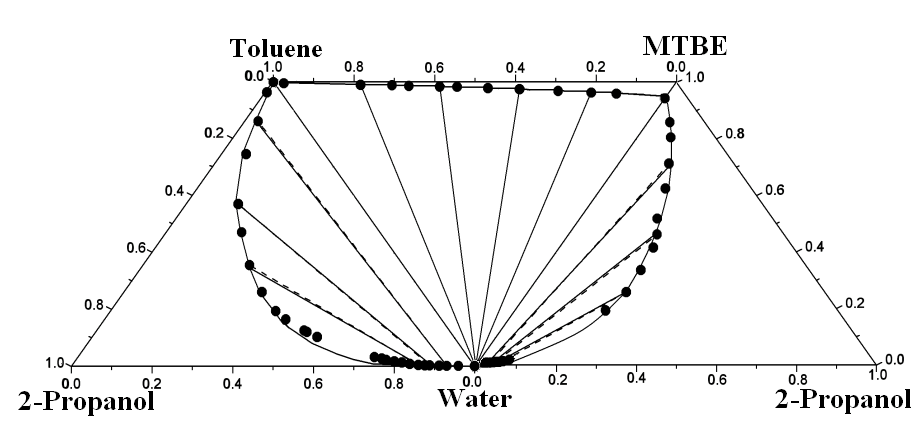
Figure 1 Experimental and calculated (liquid + liquid) equilibria of three ternary mixtures making up (water + 2-propanol + MTBE + toluene) at T = 298.15 K. ●- - -●, Experimental tie line; ——, correlated by the modified UNIQUAC model with binary and ternary parameters taken from Ttables 2 and 3.
4. CONCLUSION
The quaternary LLE of the water +
2-propanol + MTBE + toluene system were measured at 298.15 K in this work. The
experimental quaternary liquid–liquid
equilibrium data were successfully correlated by using both models including binary,
ternary and quaternary parameters. The quaternary liquid–liquid equilibrium results calculated by the modified UNIQUAC model
are in better agreement with experimental results.
REFERENCES
[1] Tamura K, Chen Y, Yamada T et al. J
Solution Chem, 2000, 29 (5): 463–488.
[2] Nagata I. Fluid Phase Equilibria, 1990, 54: 191–206.
[3] Washburn E R, Beguin A E. J Am Chem Soc, 1940, 62: 579–581.
[4] Peschke N, Sandler S I. J Chem Eng Data, 1995, 40: 315–320.
[5] Udovenko V V, Mazanko T F. Zh Fiz Khim, 1967, 41: 1615–1620.
[6] Ashcroft S J, Claylon A D, Shearn R B. J Chem Eng Data, 1979, 24: 195–199.
[7] Segura H, Galindo G, Reich R et al. Phys Chem Liq, 2002, 40 (3): 277–294.
[8] Plura J, Matous J, Novák J P et al. Coll Czechosiov Chem Commun, 1979, 44:
3627–3631.
[9] Arce A, Blanco M, Riveiro R et al. Can J Chem Eng, 1996, 74: 419–422.
[10] Ruiz F, Prats D, Gomis V. J Chem Eng Data, 1985, 30: 412–416.
[11] Pan Z J, Chen Y, Dong Y H, et al. J Jinan University 2004, 25 (5): 609–614.
[12] Prausnitz J M, Anderson T F, Grens E A, et al. Computer Calculation for
Multicomponent Vapor-Liquid and Liquid-Liquid Equilibria . Prentice-Hall: Englewood
Cliffs, NJ, 1980:19.
[13] Gmehling J, Onken U. Vapor-Liquid Equilibrium Data Collection.Vol. I, Part 1.
DECHEMA: Frankfurt / Main, 1977:327,585.
[14] Park S –J, Han K –J, Gmehline J. Fluid Phase Equilibria, 2002, 200: 399–409.
[15] Spencer C F, Danner R P. J Chem Eng Data, 1972, 17: 236–241.
[16] Hayden J G, O'Connell J P. J Ind Eng Chem Process Des Dev, 1975, 14: 209–216.
[17] Nelder J A, Mead R. J Computer, 1965, 7: 308–313.
[18] Macedo E A, Rasmussen P. Liquid-Liquid Equilibrium Data Collection (Supplement 1),
DECHEMA Chemistry Data Series, Vol. V, Part 4. DECHEMA: Frankfurt / Main, 1987.
董艳辉 陈瑶
(暨南大学化学系 广东 广州 510632)
2005年8月8日收稿。国家教育部留学回国人员科研基金(No.2002247), 广州暨南大学科研基金(No.640071) 和广东省科技计划基金(No.2003C33101)。
摘要 测定了水、异丙醇、甲基叔丁基醚和甲苯四元体系在298.15K和常压下的液液相平衡数据,含有二元、三元和四元参数的modified UNIQUAC 和 extended UNIQUAC 热力学模型成功地关联了这些实验数据。
关键词 液液平衡,含氧化合物,四元混合物,Modified和extended UNIQUAC 热力学模型