http://www.chemistrymag.org/cji/2006/085038pe.htm |
May 16, 2006 Vol.8 No.5 P.38 Copyright |
(Department of Chemistry, Shanxi Normal University, Linfen, 041004, China)
Received Mar.18, 2006; Supported by NNSFC (20471034) and Youth Foundation of Shanxi (20051011)
Abstract Transition structures, activation energies, energies differences and NICS values were calculated by ab initio quantum mechanical methods for the Cope rearrangements of a series of 1 (5)-monosubstituted semibullvalenes (1 and 2) and 1, 5-disubstituted semibullvalenes (3 and 4). In considering
p-electron donating or accepting substituents at position 1 or 5 of semibullvalenes, the calculation results are in accordance with Hoffmann's early prediction. While in the 1, 5-disubstituted semibullvalenes, which we emphasized on, p-electron groups all shift the equilibrium toward 4, as can be ascribed to the BCO stabilization effects. p-electron donors also reduce the Cope barriers in the 1, 5-disubstituted semibullvalenes. Most of the transition states (except for TS0e) are delocalized, neutral bishomoaromatic. The halogen substituents' parameters of the Cope rearrangement also have corresponding varieties with the change of the main quantum number.Keywords Transition State,Geometry Configuration,Aromaticity,Reaction Barrier,Energies Difference
1 INTRODUCTION
Fluxional semibullvalene[1] is
quite well-known for its small reaction barrier (4.8-5.2 kcal/mol)[2-3] to the
[3,3]-s shift degenerate Cope rearrangement. Semibullvalene and its
derivatives have intrigued chemists for years. A series of theoretical and experimental
studies in the Cope rearrangement have been reported[4-13]. Recently, with the
development of "boron carbonyl chemistry"[14-19], novel results have
been reported: Wu H.-S.[19] et al suggest that the barriers to the degenerate
Cope rearrangement in the semibullvalenes which are substituted by BCO at appropriate
positions are eliminated, namely, the traditional transition states have been led to
delocalized stabilities. Based on these work and the remarkable isolobal analogy[20]
between the two fragments CH and BCO, we replace CH by BCO at appropriate positions after
considering the p-electron accepters (R=CN, COH) and p-electron donors (R=F, Cl, Br,
OH) substituting at certain positions of semibullvalene, in order to study the Cope
rearrangement of semibullvalene ulteriorly and extend the emerging field of boron carbonyl
chemistry. This article will first focus on the study of 1, 5-disubstituted
semibullvalenes.
2 COMPUTIONAL METHODS
Complete geometric optimizations were done at the B3P86 levels which give better
agreement than B3LYP with the known experimental Cope barriers, by using the
6-311+G**basis set with the Gaussian 03 suite of programs[21]. Vibrational
frequencies (at B3P86/6-311+G**) were used to characterize the nature of geometries
[either were energy minima (Nimag= 0) or transition states (TS) with one imaginary
frequency (Nimag = 1)], without scaling. Nucleus independent chemical shifts (NICS)[22]
were computed at HF-GIAO/6-31+G*// B3P86/6-311+G** with G03W to indicate the aromatic
character. Considering the validity of the data, we dealt the heavy halogen substituents
with the same computational method.
3 RESULT AND DISCUSSION
Consider the Cope rearrangement equilibrium between 1-R-semibullvalenes (1) and
5-R-semibullvalenes (2). (see Fig. 1).
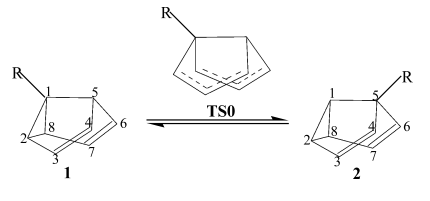
Fig. 1 The Cope rearrangement between
1-substituted semibullvalenes (1) and 5-substituted semibullvalenes (2)
In 1, the substituent R is on the
cyclopropane ring, while in 2 it is just on a normal tertiary carbon. The
cyclopropane ring moiety influences much on the stabilization of semibullvalene. In the
Walsh model, the carbon atoms of the cyclopropane are bonded with sp2
hybridization, and their residual p orbitals form cyclopropane’s HOMO frontier orbitals whose energies are higher than those of
the inner sp2 hybridized orbitals. These frontier orbitals are some closing to π
orbitals and have greater radial extension of the orbitals,
so they can easily react with π-electron accepters.
When π-electron accepters substitute on the
cyclopropane ring, the semibullvalene will be more stabilized, i.e. in Fig. 1, a π-electron accepter will shift the Cope rearrangement toward 1,
and a π-electron donor will shift the equilibrium in
the opposite direction, toward 2.
Fig. 2 gives the sketch maps of the substituted semibullvalenes (1,
2, 3 and 4) and the transition states (TS0 and TS1) for
Cope rearrangement. The computed energy differences, ΔE,
are listed in Table 1, a positive value implying that 2 (or 4) is higher in
energy and less stable than 1 (or 3), while the negative value implying the
opposite. The computed activation free energies of the Cope rearrangement, ΔG#, are listed in Table 2 and key distances are listed
in Table 3.
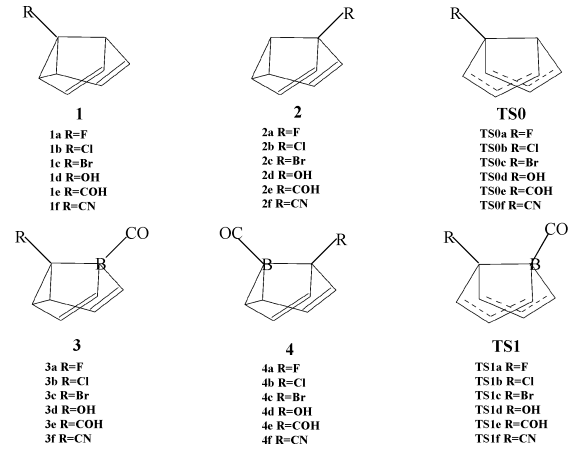
Fig. 2 The optimized structures of the
substituted semibullvalenes (1, 2, 3 and 4) and the transition
states (TS0 and TS1) for Cope rearrangement
3.1 The Direction of the Cope Rearrangement
In monosubstituted semibullvalenes, p-electron donors shift the Cope equilibrium markedly toward 2,
while p-electron
acceptors shift the equilibrium in the opposite direction, toward 1 (see Table 1). The
calculation results confirm our prediction, and greatly agreed with Hoffmann's qualitative
molecular orbital theory arguments[23]. Note that hydroxyl group shifts the
equilibrium to 1d, for it can rotate out of its original configuration to escape this
destabilization and reach the global minimum of the potential energy surface.
Table 1 Computed total Energies Differences
ΔE1/(kcal/mol) |
ΔE2/(kcal/mol) |
||
1a→2a |
-3.6 |
3a→4a |
-7.2 |
1b→2b |
-1.5 |
3b→4b |
-5.7 |
1c→2c |
-1.4 |
3c→4c |
-5.6 |
1d→2d |
0.3 |
3d→4d |
-6.0 |
1e→2e |
4.8 |
3e→4e |
-2.5 |
1f→2f |
2.6 |
3f→4f |
-2.2 |
At B3P86/6-311+G**
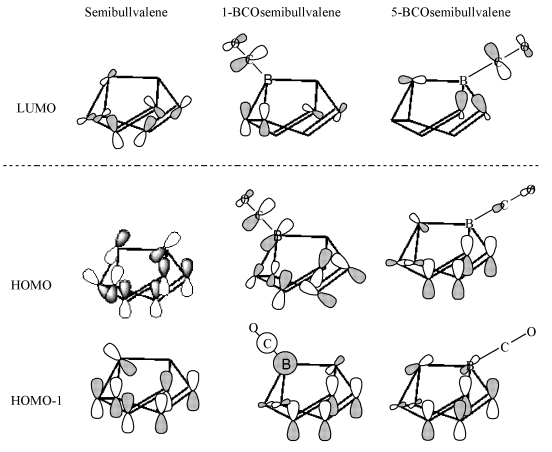
Fig. 3 The frontier molecular orbitals of
semibullvalene, 1-BCOsemibullvalene and 5-BCOsemibullvalene
In 1, 5-disubstituted
semibullvalenes, p-electron
groups all shift the Cope rearrangement equilibrium markedly toward
1-BCO-5-R-semibullvalenes (4).
It is necessary to discuss how BCO substituent influences the structure
and stability of semibullvalene by considering the frontier molecular orbitals of
semibullvalene, 1-BCO-semibullvalene and 5-BCO-semibullvalene. These relevant frontier
molecular orbitals are depicted in Fig. 3. The replacement of CH by BCO at position 5
leads to the same frontier orbitals as those of the parent semibullvalene, while the
replacement of CH by BCO at position 1 has made the original HOMO and HUMO-1 reversal. The
HOMO after substituting has lager electron density, due to the p-bond between atom B and atom C. The
greater radial extension of the orbitals favors the bridged structures and enhances the
stabilization of the semibullvalene consumedly. That is the reason for the stabilization
of 4.
In disubstituted systems, p-electron accepters make the energy differences reduced relative to
those in the corresponding monosubstituted systems. It suggests that the kinetic constant
of the Cope rearrangement equilibrium is reduced. p-electron donors make the energy differences increased, which is
advantageous to synthesize. With the reduction of electronegatiuity, the halogen
substituents’ ability to offer electrons enhances,
and the trend of the energy differences between 1 and 2 (or 3 and 4)
is declined, too.
3.2 The Reaction Barrier
Vide supra, in the monosubstitued systems, p-electron donors (F, Cl, Br) shift the Cope equilibrium toward 2.
Their Cope barriers reduced (0.5, 1.9 and 1.8 kcal/mol, respectively) drastically,
relative to that of the parent semibullvalene (5.0 kcal/mol). The hydroxyl group and p-electron accepters (COH, CN)
also reduce their Cope barriers (2.8, 2.6 and 4.3 kcal/mol, respectively). These small
barriers suggest that appropriate substituents at appropriate positions of semibullvalene
might stabilize the transition state to an energy minimum.
| DG#/(kcal/mol) | D G#/(kcal/mol) |
||
1a→TS0a |
0.5 |
2a→TS0a |
6.7 |
3a→TS1a |
2.8 |
4a→TS1a |
9.0 |
1b→TS0b |
1.9 |
2b→TS0b |
3.5 |
3b→TS1b |
4.3 |
4b→TS1b |
9.0 |
1c→TS0c |
1.8 |
2c→TS0c |
3.2 |
3c→TS1c |
4.1 |
4c→TS1c |
8.8 |
1d→TS0d |
3.1 |
2d→TS0d |
2.8 |
3d→TS1d |
3.7 |
4d→TS1d |
8.8 |
1e→TS0e |
7.7 |
2e→TS0e |
2.6 |
3e→TS1e |
8.4 |
4e→TS1e |
9.9 |
1f→TS0f |
6.7 |
2f→TS0f |
4.3 |
3f→TS1f |
8.1 |
4f→TS1f |
9.6 |
At B3P86/6-311+G**
In the disubstituted systems, p-electron donors (F, Cl, Br, OH) reduce the activation free energies (2.8, 4.3, 4.1 and 3.7 kcal/mol, respectively), while π-electron accepters (COH, CN) increase the barriers (8.4 and 8.1 kcal/mol, respectively). However, the activation barriers to the Cope rearrangement are increased in the disubstituted semibullvalenes, compared with those in the monosubstituted semibullvalenes. That was caused by the enhanced stabilization of both transition states and reactants, but the latter more so.3.3 The Geometry Configuration and Aromatic
Character
The distance between atom 2 and atom 8 is an important geometry index of the effects
of the substituents. In the monosubstituted semibullvalenes, if R is a p-electron accepter, it will
strengthen the 2-8 bond in 1 but will have little effects on 2. Thus 1 should be more
stable than 2. Similarly if R is a p-electron donor it will weaken the 2-8 bond of 1 and shift the Cope
equilibrium to 2[23]. By calculation, we find that the same argument can be
applied to the disubstituted semibullvalenes. As shown in Table 3, the R2,8
values of 1a, 3a, 1b, 3b, 1c, 3c, 1d, 3d (1.670,1.648,1.631, 1.623, 1.633, 1.624, 1.603 and 1.639Å, respectively)
are evidently longer than that of the parent semibullvalene (1.601Å). There are no
typical R2,8 single bonds in these configurations. The reason for that is the
weak combination of the frontier orbitals of cyclopropane ring and p-electron donors. We can also find that
the eigenvalues of R2,8 of 3 are shorter than those in 1, which can be ascribed
to the BCO stabilization effects at the bridging position 5 of semibullvalene.
Nimag |
R2,8/(Å) | R2,3/(Å) | R3,4/(Å) | R4,6/(Å) | NICS/(ppm) |
|
1a/ Cs |
0 |
1.670 |
1.459 |
1.345 |
2.331 |
-12.7 |
2a/ Cs |
0 |
1.618 |
1.463 |
1.344 |
2.345 |
-12.9 |
TS0a/ Cs |
1 |
1.973 |
1.412 |
1.366 |
2.217 |
-20.8 |
3a/ Cs |
0 |
1.648 |
1.464 |
1.348 |
2.542 |
-11.8 |
4a/ Cs |
0 |
1.536 |
1.475 |
1.341 |
2.349 |
-8.8 |
TS1a/ Cs |
1 |
2.152 |
1.397 |
1.383 |
2.148 |
-22.6 |
1b/ Cs |
0 |
1.631 |
1.463 |
1.342 |
2.34 |
-11.3 |
2b/ Cs |
0 |
1.616 |
1.463 |
1.343 |
2.338 |
-11.9 |
TS0b/ Cs |
1 |
2.069 |
1.395 |
1.378 |
2.144 |
-22.3 |
3b/ Cs |
0 |
1.623 |
1.466 |
1.346 |
2.547 |
-10.9 |
4b/ Cs |
0 |
1.535 |
1.475 |
1.341 |
2.347 |
-8.0 |
TS1b/ Cs |
1 |
2.131 |
1.383 |
1.397 |
2.140 |
-22.3 |
1c/ Cs |
0 |
1.633 |
1.463 |
1.342 |
2.340 |
-11.2 |
2c/ Cs |
0 |
1.615 |
1.463 |
1.343 |
2.339 |
-11.6 |
TS0c/ Cs |
1 |
2.102 |
1.391 |
1.381 |
2.123 |
-21.8 |
3c/ Cs |
0 |
1.624 |
1.467 |
1.346 |
2.547 |
-10.7 |
4c/ Cs |
0 |
1.535 |
1.474 |
1.342 |
2.348 |
-7.8 |
TS1c/ Cs |
1 |
2.136 |
1.382 |
1.397 |
2.140 |
-22.2 |
1d/ C1 |
0 |
1.635 |
1.462 |
1.343 |
2.333 |
-11.9 |
2d/ C1 |
0 |
1.615 |
1.463 |
1.343 |
2.335 |
-12.3 |
Ts0d/ C1 |
1 |
2.053 |
1.396 |
1.379 |
2.130 |
-22.7 |
3d/ Cs |
0 |
1.639 |
1.465 |
1.347 |
2.542 |
-11.1 |
4d/ Cs |
0 |
1.535 |
1.474 |
1.341 |
2.342 |
-8.4 |
Tsd1/ C1 |
1 |
2.137 |
1.396 |
1.384 |
2.127 |
-24.7 |
1e/ Cs |
0 |
1.558 |
1.471 |
1.340 |
2.347 |
-9.4 |
2e/ C1 |
0 |
1.605 |
1.466 |
1.341 |
2.336 |
-11.0 |
Ts0e/ Cs |
1 |
2.072 |
1.381 |
1.391 |
2.016 |
-11.3 |
3e/ Cs |
0 |
1.552 |
1.471 |
1.343 |
2.547 |
-29.3 |
4e/ C1 |
0 |
1.526 |
1.475 |
1.339 |
2.363 |
-7.0 |
TS1e/ C1 |
1 |
2.097 |
1.384 |
1.393 |
2.143 |
-22.5 |
1f/ Cs |
0 |
1.577 |
1.470 |
1.339 |
2.346 |
-9.7 |
2f/ Cs |
0 |
1.603 |
1.464 |
1.340 |
2.343 |
-11.1 |
TS0f/ Cs |
1 |
2.080 |
1.383 |
1.387 |
2.048 |
-23.4 |
3f/ Cs |
0 |
1.576 |
1.471 |
1.343 |
2.545 |
-9.8 |
4f/ Cs |
0 |
1.530 |
1.473 |
1.338 |
2.355 |
-7.6 |
TS1f/ Cs |
1 |
2.118 |
1.394 |
1.381 |
2.083 |
-23.1 |
We also pay attention to the geometric
configuration of the transition states, see Fig. 4, each of whom has an imaginary
frequency (Nimag=1). Whether in the monosubstitued or the disubstituted systems, the C-C
bonds around the periphery of a Cope system are of approximately equal length. The average
lengths of C-C bonds (Rav) are between the value of single bonds (1.54Å)
and the value of the double bonds (1.34Å), more close to the double ones. The Rav
values of the disubstituted semibullvalenes are all increased relative to those in
monosubstituted semibullvalenes, which indicate that the replacement of CH by BCO favors
the delocalized semibullvalenes substantially. Due to the interaction of the symmetric
combination of the allyl nonbonding orbitals with an antibonding skeletal orbital, the C1-C5
bonds (R1,5) of the disubstituted semibullvalenes are weakened, and the R1,5
bond lengths are elongated.
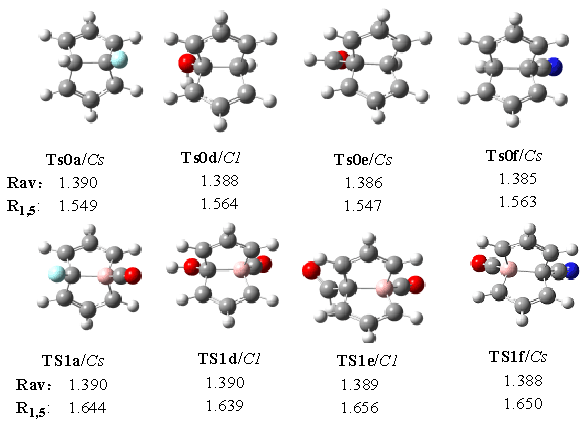
Fig. 4 Structures and bond lengths of some
transition states
On the base of the geometric,
energetic, and the nucleus independent chemical shifts, NICS, Cs semibullvalene
itself is not aromatic, but its C2v transition state for the Cope rearrangement
is highly neutral bishomoaromatic[24-27]. The cyclopropane unit in
semibullvalene is largely responsible for the NICS value and there is no significant
contribution from homoconjugation. The C2v transition state's calculated NICS
value of geometric center of the active atoms (C2, 3, 4, 6, 7, 8) is -22.7.
Once deleting the contribution of the cyclopropane ring, the NICS value of the C2v
transition state is still largely negative. After substituting, as shown in Table 3, all
the transition states have largely negative NICS values. They are all delocalized, neutral
bishomoaromatic. The substitutions we have done are at the bridging 1,5-positions that are
not in the Cope active system in semibullvalene, which do little contribution to the
aromaticity, so the NICS values are almost as much as that of the parent system.
Interestingly, 3e has the largest negative NICS value (-29.3), while TS0e
has little NICS value (-11.3). The cause is that 3e has aromatic character, while
its theoretic transition state has no aromatic character.
With the enhancement of the main quantum numbers, the halogen
substituents will reduce the overlap of the p orbitals between themselves and the carbons,
which causes the reduction of the delocalization of electron and the smaller NICS value.
Take 1 for example, the order of the NICS value is as follows: 1a
(-12.7)>1b (-11.3)>1c (-11.2). The NICS values of the 1b and 1c
are almost the same, which is caused by the deflection of computational methodology. In
theory, 1c should have smaller NICS value.
4 CONCLUSION
Calculations on the 1 (5)-monosubstitued semibullvalenes, 1, 5-disubstituted
semibullvalenes and their transition states for the Cope rearrangement with the Gaussian
03 suite of programs were carried out. The energy differences show that in the
disubstituted semibullvalenes, π-electron groups
shift the Cope rearrangement toward 1-BCO-5-R- semibullvalenes (4). π-electron donors substituting on the position 1 or 5 of
semibullvalene also reduce the Cope barriers relative to that of the parent semibullvalene
in the disubstituted semibullvalenes. Most of the transition states are delocalized,
neutral bishomoaromatic. Frontier molecular orbital theory and the geometrical features of
the transition states elucidate the effects of BCO substitutent. With the change of the
main quantum number, the halogen's series parameters of the Cope rearrangement have
corresponding varieties. A series of such work will be reported in the future.
REFERENCES
[1] Zimmerman, H. E.; Grunewald, G. L. J.
Am. Chem. Soc. 1966, 88: 183.
[2] Cheng, A. K.; Anet, F. A. L.; Mioduski, J.; Meinwald, J. J. Am. Chem.Soc. 1974, 96:
2887.
[3] Moskau, D.; Aydin, R.; Leber, W.; Günther, H.; Quast, H.; Martin, H.-D.; Hassenrück,
K.; Miller, L. S.; Grohmann, K. Chem. Ber. 1989, 122: 925.
[4] Zimmerman, H. E.; Binkley, R. W.; Givens, R. S.; Grunewald, G. L.; Sherwin, M. A. J.
Am. Chem. Soc. 1969, 91: 3316.
[5] Meinwald, J.; Tsuruta, H. J. Am. Chem. Soc. 1969, 91: 5878.
[6] Miller, L. S.; Grohmann, K.; Damenberg, J. J. J. Am. Chem. Soc. 1983, 105: 6862.
[7] Brown, E. C.; Henze, D. K.; Borden, W. T. J. Am. Chem. Soc. 2002, 124: 14977.
[8] Dohle, M.; Manz, j.; Paramonov1, G.K.; Quast, H. Chemical Physics. 1995, 197: 91.
[9] Goren, A. C.; Hrovat, D. A.; Seefelder, M.; Quast, H.; Borden, W. T. J. Am. Chem. Soc.
2002, 124: 3469.
[10] Cheng, A. K.; Anet, F. A. L.; Mioduski, J.; lb, Meinwald, J.; J. Am. Chem. Soc. 1974,
124: 3469.
[11] Williams, R. V. Chem. Rev. 2001, 101: 1105.
[12] Williams, R. V.; Gadgil, V. R.; Chauhan, K. J. Org. Chem. 1998, 63: 3302.
[13] Heubes, M.; Dietz, T.; Quast, H.; Seefelder, M.; Witzel1, A. J. Org. Chem. 2001, 66:
1949.
[14] Zhou, M.; Tsumori, N.; K, Z. Li. J. Am. Chem. Soc. 2002, 124: 12936.
[15] Papakondylis, A. J. Phys. Chem. A. 2004, 108: 4335.
[16] Wu, H.-S.; Jiao, H.; Wang, Z. X.; Schleyer, P. v R. J. Am. Chem. Soc. 2003, 125:
4428.
[17] Wu, H.-S.; Qin, X.-F.; Jiao, H.; Schleyer, P. v. R. J. Am. Chem. Soc. 2005, 127:
2334.
[18] Chen, M.; Kong, Q.; Zhou, M. Journal of Molecular Structure 2003, 657: 101.
[19] Wu, H.-S.; Jiao, H.; Wang, Z. X.; Schleyer, P. v. R. J. Am. Chem. Soc. 2003, 125:
10524.
[20] Hoffmann, R. et al. Angew. Chem. Int. Ed. Engl. 1982, 21: 711.
[21] Frisch, M. J. et al. Gaussian, Inc., Pittsburgh PA, 2003.
[22] Jiao, H.; Nagelkerke, R.; Kurtz, H. A.; Williams, R. V.; Borden, W. T.; Schleyer, P.
v. R. J. Am. Chem. Soc. 1997, 119: 5921.
[23] Hoffmann, R.; Stohrer, W. D. J. Am. Chem. Soc. 1971, 93: 6941.
[24] Williams, R. V.; Theor. AdV. Interesting Mol. 1998, 4: 157.
[25] Williams, R. V. Eur.J. Org. Chem. 2001, 227.
[26] Rao, S. N.; More O’Ferrall, R.
A.; Kelly, S. C.; Boyd, D. R.; Agarwal, R. J. Am. Chem. Soc. 1993, 115: 5458.
[27] Jia, Z.S.; Brandt, P.; Thibblin, A. J. Am. Chem. Soc. 2001, 123: 10147.
裴晓琴 张晓清 武海顺
(山西师范大学化学与材料科学学院 临汾 041004)
摘要 运用从头计算量化方法对一系列进行Cope 重排的1(或5)-单取代半瞬烯(1 和2),以及1,5-二取代半瞬烯(3和4)的过渡态结构、活化能、能量差和核独立化学位移值进行了计算。在1(或5)-单取代半瞬烯体系里,π电子基对其Cope重排的影响与Hoffmann早年的定性预测非常吻合。我们重点讨论了π电子基与BCO共同取代的1,5-二取代半瞬烯体系,由于BCO在桥位置上的稳定效应,π电子基均使得Cope重排向4进行,并且π给电子基还使其活化能降低。多数过渡态(除TS0e)都是离域,双同芳香性的。随着卤素主量子数的变化,它们的取代半瞬烯Cope重排相关参数也有相应的规律性变化。
关键词 过渡态,几何构型,芳香性,活化能,能量差