Computer simulation of conic-shaped patterns on fracture surfaces of polymers

Luo Wenbo, Yang Tingqing^#
(Institute of Fundamental Mechanics and Material Engineering, Xiangtan University, Xiangtan 411105, China；^#Department of Mechanics, Huazhong University of Science and Technology, Wuhan 430074, China)

1. INTRODUCTION
Polymer glasses are attractive materials for many engineering applications, as they are low in density, have excellent mechanical properties and are easily fabricated by processes such as injection molding, extrusion and vacuum forming. Their stiffness and strength must satisfy the structural needs. Therefore the failure theory of polymers attracts many researchers' attention. During the fracture process, a craze or shear yielding zone usually forms at a crack tip^[1]. The initiation, growth and breakdown of crazes or shear yielding zones are thus central to understanding of the fracture mechanics of polymer glasses. There are two main methods to study the process of craze growth and craze breakdown. One is optical interferometry used to measure the size and shape of single crack tip crazes in transparent polymers ^[2,3]. The results of interferometric measurements are used in connection with fracture mechanics models and mathematical or numerical methods for calculations of stress in the micro-region at the crack tip and thus giving qualitative and quantitative descriptions of deformation and fracture processes. The other is fractographic analysis of fracture surfaces, which is an important and often used method to investigate the failure mode and damage-fracture mechanism ^[4-12]. Fracture process of many glassy polymers is usually associated with craze formation and governed by craze growth and breakdown. There are several distinct patterns on fracture surfaces, such as radial striations, regularly spaced 'rib' markings and conic-shaped patterns, etc. They are related to distinct deformation and fracture mechanisms. The conic-shaped pattern is thought to be the intersection locus of a moving planar crack front and a growing circular craze or secondary crack front ^[1,9-11]. In this paper, the effects of the ratio of crack velocity to craze or secondary crack velocity on the shape of intersection loci are discussed via computer simulations.

2. DISTINCT PATTERNS ON FRACTURE SURFACES OF POLYMERS
For a slow moving crack/craze entity in polymethyl methacrylate (PMMA), crack growth takes place by breakdown of the craze along its midrib which leaves a relatively smooth fracture surface ^[13,14] and dissipates relatively small amount of energy to create new surfaces. During the continuous loading, the crack growth speeds up, and the fracture surfaces have regularly spaced 'rib' markings perpendicular to the direction of crack growth ^[15,16], which appears to be related to a type of stick/slip propagation due to either crack bifurcation or the effect of stress waves ^[15]. The transition between these two distinct types of surface morphology can be very abrupt. For some other materials such as polystyrene (PS), polycarbonate (PC), acrylonitrile-butadiene- styrene (ABS) copolymer, polypropylene (PP), high-density polyethylene (HDPE) and epoxy resin, there exist more features on their fracture surfaces ^[4-17]. Conic-shaped patterns ^[9-11,17] are often seen on the fracture surfaces when relatively slow crack growth has taken place as shown in figure 1. For rapidly moving cracks in these materials irregular 'mackerel' or 'patch' patterns are found on fracture surfaces ^[1,8,11,14].

    The conic-shaped surface patterns are thought to be the intersection loci of the moving planar crack front and growing circular crazes or secondary cracks, as illustrated schematically by figure 2. The parallel lines represent the moving crack front and the concentric circles represent the radially growing craze or secondary crack front. It can be seen in figure 2 that the points of intersection in time sequence form a conic-shaped pattern, aligned with the bow of the conic section pointing towards the moving crack. Craze or secondary crack initiates at the focal point of the conic section. The initiation site, which is the location of stress concentration due to material inhomogeneity (e.g. secondary particles), can be clearly seen in figure 1(c). The number of conic-shaped patterns is dependent on the degree of material inhomogeneity and the loading conditions. It has been shown that the shape of conic section is dependent on the ratio of crack velocity to craze or secondary crack velocity, .

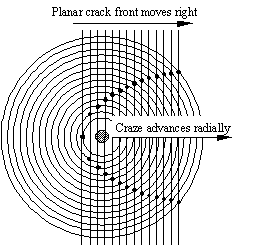
Fig. 2 Sketch of the conic-shaped pattern

3. COMPUTER SIMULATION OF CONIC-SHAPED PATTERNS       
The computer simulation of conic-shaped patterns on fracture surfaces is given below based on their formation mechanisms. In methodology it means to solve a system of equations that describe the motion of the moving fronts of main crack and crazes or secondary cracks. As shown in figure 2, the main crack is supposed to propagate right with velocity of , and the craze or secondary crack advances radially with velocity of . The hatched circle in figure 2 indicates the craze initiation site. The radius of the craze or secondary crack front (represented by circle in figure 3) is assumed to reach at the instant when the main crack front first meets the front of craze or secondary crack, i.e. when the first left line is exactly the tangent line of the smallest circle as shown in figure 2. By constructing a coordinate system with its origin at the craze initiation site and the x axis parallel to the crack growth direction, we can give the control equations for crack front growth and craze front advance as follows
for crack front growth (1)
for craze front advance (2)
in which t is time. Substituting Eq.(1) into Eq.(2) yields
(3)
Eq.(3) is the control equation for the intersection loci of the moving planar crack front and growing circular crazes or secondary cracks. It has a conic form, but the specific shape depends on the ratio of crack velocity to craze or secondary crack velocity, .



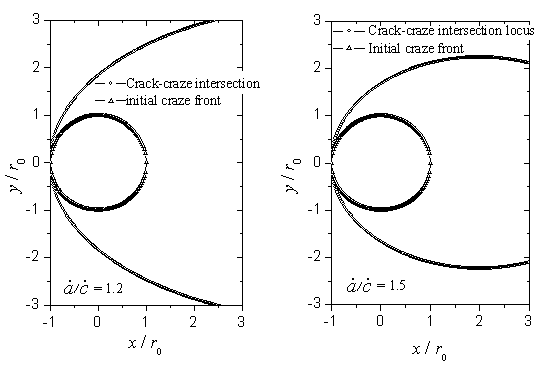
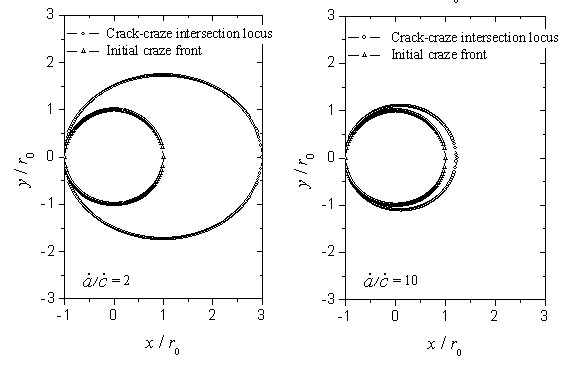
Fig. 3 Computer simulation of conic-shape patterns on fracture surfaces for different

    In figure 3 it is shown the variation of the shape of the conic-shaped patterns. The simulated patterns are limited in a rectangular area with size of . From figure 3, it can be seen that when the ratio, , increases progressively, the fracture surface pattern changes from a parabola or a prolate parabola to an ellipse and finally to an approximate circle.
    Figure 4 shows the fracture surface morphology near a crack root and its simulation result for a dual edge notched PP specimen under tension with constant displacement rate. In simulation we let r₀=50mm,=4/3. It can be seen from figure 4(a) that several crazes form near the crack root due to stress concentration and material inhomogeneity and they distribute in a regular spaced manner along the specimen width. During the continuous loading, the crazes grow and simultaneously the crack propagates slowly, their fronts intersect each other and form the parabola patterns. When the instability criterion for crack growth is met, the crack propagates at a very high speed and the crazes initiated near the crack front have no enough time to grow. Thus a large number of fine near circle patterns are left on the fracture surface (see figure 5).

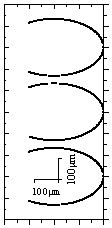(a)         (b)
rapid crack    slow crack      prefabricated
growth zone   growth zone   crack plane
Fig.4 (a) Parabolic patterns on fracture surface of PP; (b)computer simulation


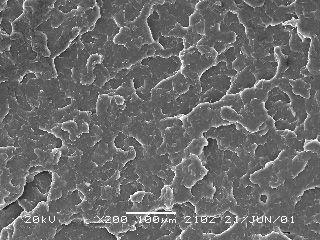
Fig.5 Surface patterns in rapid fracture  region of PP specimen in Fig.4(a)

4. CONCLUDING REMARKS
Fracture surface morphology analysis is an important method to investigate the failure modes and damage-fracture mechanisms of polymers. The conic-shaped pattern is the intersection locus of a moving planar crack front and a radially growing circular craze or secondary crack front. Its shape is dependent on the ratio of crack velocity to craze or secondary crack velocity, . It is shown from the computer simulations that when the ratio, , increases progressively, the fracture surface pattern changes from a parabola or a prolate parabola to an ellipse and finally to an approximate circle.

REFERENCES          
[1] Kinloch A J, Young R J. Fracture Behaviour of Polymers, Applied Science Publishers, London and New York, 1983.
[2] Doll W, Konczol L. In: Advances in Polymer Science, 91/92, (Ed. By Kausch H H), Berlin: Springer, 1990, 137-214.
[3] Schirrer R. In: Advances in Polymer Science, 91/92, (Ed. By Kausch H H), Berlin: Springer, 1990, 215-262 .
[4] Narisawa I, Ishkawa M. In: Advances in Polymer Science, 91/92, (Ed. By Kausch H H), Berlin: Springer, 1990, 353-391.
[5] Li J X, Hiltner A, Baer E. J. Appl. Polym. Sci., 1994,52:269.
[6] Tanrattanakul V, Perkins WG, Massey FL. J. Mater. Sci., 1997,32:4749.
[7] Liu K, Piggott M R. Polym. Eng. Sci., 1998,38:69.
[8] Reynolds P T. J. Mater. Sci. Letters, 1988,7:759.
[9] Lee E K C, Rudin A. Plumtree A. J. Mater. Sci., 1995,30:209.
[10] Kulawansa D M, Langford S C, Dickinson J T. J. Mater. Res., 1992,7:129.
[11] Lu X C. Strength and failure of polymeric materials (Gaojuwu De Qiangdu Yu Pohuai ), Chengdu: Sichuan Education Press (Sichuan Jiaoyu Chubanshe),1988.
[12] Van Der Zwet M J M, Heidweiller A J. J. Appl. Polym. Sci.,　1998,67:1473.
[13] Doyle M J. J. Mater. Sci., 1982,17:760.
[14] Lauterwasser B D, Kramer E J. Phil. Mag., 1979,A39:468.
[15] Kusy R P, Lee H B, Turner D T. J. Mater. Sci., 1976,11:118.
[16] Cheng Chihmin, Hiltner A, Baer E, et. al.. J. Appl. Polym. Sci., 1994,52:177.
[17] Zhang M J, Zhi F X, Su X R. Polym. Eng. Sci., 1989,29: 1142.

[ Back ] [ Home ] [ Up ] [ Next ]Mirror Site in USA  Europe  China  GBNet