http://www.chemistrymag.org/cji/2003/053027ne.htm |
Mar. 1, 2003 Vol.5 No.3 P.27 Copyright |
(Department of Physics, Zhejiang University, Hangzhou 310028, China; #Department of Physics, Wenzhou University, Wenzhou, 325027, China)¡¡ Received Dec. 9, 2002; Supported by the National Natural Science Foundation of China(Grant No. 20204014). Abstract The probability distribution P(A, S) of linear polymer chains on simple cubic(SC) lattice is investigated using dynamic Monte Carlo technique, here A and S are the asphericity and the radius of gyration respectively. Results show that a positive correlation between A and S exists for polymer chain, which is confirmed by investigating the dependence of the size <S2> and the shape <A> of polymer chain near a flat surface.
Keywords Polymer, Probability distribution, Monte Carlo simulation 1. INTRODUCTION
Flexible polymer chains can assume a large number of configurations owing to many internal degrees of freedom. As early as 1934, Kuhn pointed out that the instantaneous spatial configurations of polymer chains in dilute solutions were highly anisotropic, though isotropy were acquired over long times through orientational averaging or over a great number of configurations [1]. The study on the shape of polymer chains has been of great interest to chemists as well as physicists, since the anisotropy of polymers has important physical consequences and is critical in the interpretation of viscous flows and other hydrodynamical phenomena of dilute solutions of macromolecules.
Recently, it has been found that there exists a positive correlation between the asphericity parameter A and the size (measured by the square end-to-end distance R2 or the square radius of gyration S2) for linear random walking (RW) and self-avoiding walking (SAW) chain on lattices [2,3]. Here the asphericity parameter A is defined as
(1)in three dimensions, which ranges from zero for spherically symmetric chain configurations to one for rod-shaped ones, while values L12, L22 and L32 (L1 <L2 <L3) are three components of the squared radius of gyration [4]. The correlation reveals that a chain of large size (R2 or S2) has a much more possibility to have a big asphericity parameter A, vice versa. Then, the change in chain's shape is always related with that in chain's size, that is important in studying the hydrodynamical phenomena of polymer in solution. In order to quantitatively measure the correlation, we introduced the correlation function and measured it for linear RW and SAW chain on lattices [3,5].
In this work, the probability distribution P(A, S) is studied for RW chain on simple square lattice using dynamic Monte Carlo (MC) technique. The distribution P(A, S) gives us much more detail about the correlation and mean values <A> and <S2> can be figured out from P(A, S) as
(2)and
(3)respectively. The results indicate that there exists a positive correlation between A and the size. The relationship is then confirmed by investigating the RW chain near a flat surface.
2. CHAIN MODEL AND CALCULATION METHOD
A polymer chain, comprised of n + 1 segments (n bonds) consecutively linked
with bond length l = 1 in the simple cubic lattice unit, is firstly generated
randomly with the Monte Carlo method. Afterwards, a segment is chosen randomly
and one of the three elementary motions: the end-segment, normal-segment and 90¡ã
crankshaft motions, is attempted. This motion method was discussed in detail by Gurler et
al [6] earlier. Each trial move is called a segment cycle, and n + 1
segment cycles consist of one Monte Carlo step (MCS). To avoid the correlation between two
consequent configurations, we measure the chain'
The radius of gyration tensor S is calculated by
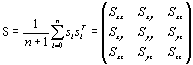, (4)here
is the position of segment i in a frame of
reference with its origin at the center of mass. The tensor S can be
diagonalized to form a diagonal matrix with three eigenvalues L12,
L22 and L32 (L1 <L2
<L3). Then, the square radius of gyration can be calculated as 
(5)
3 RESULTS
AND DISCUSSION3.1 Correlation coefficients
At first, we calculate the correlation coefficients
for the RW chain on the simple cubic(SC) lattice. To this
end, the Monte Carlo simulations are carried out for the chain of length n ranged from 10
to 500. The correlation coefficient is
calculated as
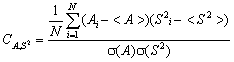(6)Here s (A) and s (S2) are the standard errors, and <A> and <S2> are the mean values. Here N = 1000¡Á100 is the total number of independent chain configurations.
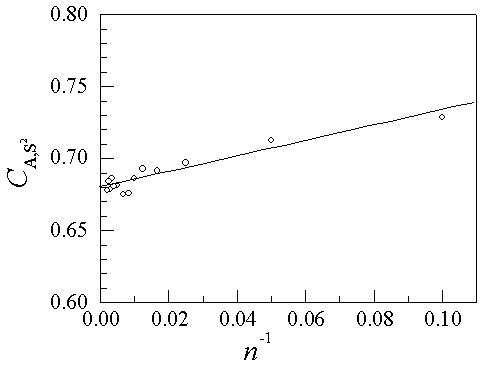
Fig.1 Correlation coefficient
of RW chain plotted as a function of inverse chain length n-1.
Circle: MC results. Solid line is the linear fit.
Figure 1 shows the
dependence of 
on the chain length n.
The positive values of indicates a positive
correlation between the asphericity parameter A and the size for polymer chain,
which means that the shape of a chain conformation of small size is often more spherical
than that of large size. The MC simulation result is consistent with the recent findings
for the chain on the tetrahedral lattice [3].
3.2 Probability distribution P(A, S)
In order to have a good understanding of the correlation between chain size and its shape,
we have also investigated the probability distribution with respect to asphericity A
and radius of gyration S, i.e. P(A, S). Figure 2 presents the
probability distribution for the RW chain with chain length n = 200. The sample
size is 5´ 106, which is larger than that for averaging. Figure 3 shows
three-dimensional probability distribution of P(A, S). From Fig. 3,
one can easily see that most configurations locate along the diagonal of the A-S
plane, i.e., have either small A and S or big A and S.
The total chain configuration samples shown in Fig 2 and Fig 3 can be
divided into four parts according to their square radius of gyration S2
and asphericity parameter A as shown in Fig. 2: (a) S2 < <S2>
and A < <A>, (b) S2 > <S2>
and A > <A>, (c) S2 < <S2>
and A > <A>, and (d) S2 > <S2>
and A < <A>. From the definition of the correlation coefficient in
Eq. 6, one can see that the contributions to the correlation coefficient 
of the first two parts are positive while the
others are negative. We find that the probability of finding the configuration in these
four parts are about 0.4382, 0.3062, 0.1729 and 0.0827 respectively for the RW chain of n
= 200. It is clear that, the probabilities of the first two parts (a and b)
are much larger than those of the last two parts (c and d). That is, among
all the chain configurations, the probability of finding a configuration with S2
< <S2> and A < <A> or with S2
> <S2> and A > <A> is much larger,
revealing the existence of the positive correlation between A and S2.
Fig.2 Probability distribution P(A, S) of the RW chain with chain length n=200. From the center to the circumference, the probability is 0.0005, 0.0004, 0.0002, 0.0001, 0.00005, 0.00002, 0.00001 and 0.000001, respectively. The total samples of the chain configuration is 5¡Á106.
Fig.3 3D plot of the probability distribution P(A, S) of the RW chain with chain length n = 200. The total samples of the chain configuration is 5¡Á106.
Fig.4 MC results of the mean square radius of gyration <S2> (left-hand scale) and the mean asphericity parameter <A> (right-hand scale) plotted vs. the distance z0 of the first segment of chain from a flat surface for the RW chain of length n = 400. 3.3 Chain near a flat surface
As an example of the correlation, we investigate the chain size and asphericity of a chain near a flat surface. The behavior of a polymer chain, confined to a restricted spatial region, is of importance for many practical problems. The mean size (<R2> and <S2>) of a random-flight chain near an impermeable, infinite large planar surface was studied earlier by Tanaka [7]. Assuming that the noninteracting surface lies at z = 0 of orthogonal coordinate system (X, Y, Z), Tanaka demonstrated that both <R2> and <S2> depend on z0, the distance of the first segment of chain from the surface. But how the shape depends on z0 is still not investigated. From the fact that the mean asphericity parameter <A> is correlated with size <S2>, one could expect that <A> behaves the same as that <S2> does. To validate this expectation, we have investigated the dependence of <S2> and <A> on z0 for the RW chain on the SC lattice, and taken the chain length n = 400 as an example here. The results are shown in Figure 4. It is clear that <S2> and <A> have almost the same behavior, indicating that the conclusion of correlation is also valid for the geometrical constrained chain. 4. CONCLUSION
The correlation between shape and size is studied using dynamic MC technique for linear RW chain on the simple cubic lattice. A positive correlation between the asphericity parameter A and chain size is found and confirmed from some aspects: such as the probability distribution P(S, A) and the RW chain near a flat surface. REFERENCES
[1] Kuhn W. Kolloid-Z., 1934, 68: 2.
[2] Zifferer G. J. Chem. Phys., 1998, 109: 3691.
[3] Luo M B, Huang J H, Chen Y C et al. Eur. Polym. J., 2001, 37: 1587.
[4] Solc K, Stochmayer W H. J. Chem. Phys., 1971, 54: 2756.
[5] Luo M B, Qian C J, Xu J M. Chemical Journal of Chinese University (Gaodeng Xuexiao Huaxue Xuebao), 2002, in press.
[6] Gurler M T, Crabb C C, Dahlin D M et al. Macromolecules, 1983, 16: 398.
[7] Tanaka T. Macromolecules, 1977, 10: 51. ¡¡