Peng Changjun, Li Jiankang, Liu Honglai, Hu Ying
(Department of Chemistry, East China University of Science and Technology, Shanghai, 200237, China)

Received Mar. 14, 2003; Supported by the National Natural Science Foundation of China (Projects No.20025618, 20236010), and the Education Committee of Shanghai City of China

Abstract Monte Carlo simulations for the adsorption of block copolymers in nonselective solvent at solid-liquid interface have been performed on a simple lattice model. In simulations, block copolymer molecules are modeled as self-avoiding linear chains composed of m segments of A and n segments of B and the segment A is attractive, while the segment B is non-attractive to the surface. Block copolymer molecules are,and, respectively. The aim of this work is to provide a systematic comparison between diblock and triblock copolymer to study the influence of the sequence of copolymer to adsorption behavior including the size distribution of loops, tails and trains configurations, the density profiles, the surface coverage, adsorbed amount and adsorption layer thickness. The results show that the size distribution of train and tail configuration for,and all present two peaks. The peak intensity and position is determined by the sequence of copolymer and the reduced adsorption energy. can easily form bigger loop configuration. The surface coverage and adsorbed amount are also affected by the sequence of copolymer. Copolymer has the highest adsorbed amount, while copolymeralways gives the smallest surface coverage and adsorbed amount as well as adsorbed layer thickness.
Keywords Block copolymers, Surface adsorption, Monte Carlo simulation

1. INTRODUCTION                  
The behavior of polymeric materials near a solid surface is very different from that in the bulk because of the existences of strong entropic constraints placed upon the polymer chain conformations near a bounding impenetrable surface. Many technological processes such as the stabilization of various commercial dispersions, surface treatment of materials and lubrication need understanding of the microscopic information around an interface, especially, the microstructure of adsorption layers in which polymers interact with the materials. Block copolymers composed of two or more kinds of segments with different physical and chemical properties usually exhibit amphiphilic behavior. This makes them a good model for the study of surfactants, especially nonionic and amphiphilic surfactants. A series of computer simulations of adsorption behavior have been reported in the literatures for diblock copolymers^[1-9] and for triblock copolymers^[10-13], Much information about microstructure of adsorbed layers including different adsorbed configurations and their distribution can be provided naturally and intuitively with the aid of computer simulation. Recently, a review on the simulation studies of polymer blends at interface has been given by Muller and Schmid^[7]. In the following we briefly mention some examples about simulation studies of adsorption behavior for triblock copolymer.
    Balazs and Lewandowski^[10] have developed computer simulations to model the adsorption of copolymer. They studied how the surface coverage is affected by the length of the B segment, copolymer concentration, A-A type associations, energy of interaction between the B segment and the surface, polydispersity, and reversible adsorption. The results have shown that self-assembly in triblock copolymers affects the behavior of these chains near an interface, and, self-association between A segments affects the extent of the surface coverage as well as the microstructure of the interfacial region. However, many other information of adsorption such as the size distribution of different configurations (train, loop and tail), adsorption amount and isotherms was not given. Misra and Mattice^[11] investigated the adsorption behavior for at solid-liquid interface. The effects of the separation of the surfaces, number of segments in a chain and the interaction between the chain end and the surface are explored. They found that there is a well-defined threshold surface separation at which bridges first appear and this separation threshold appears to be independent of energy in the semi dilute region. Nguyen-Misra et al^[12] examined adsorption and bridging by triblock copolymer chains confined between two parallel flat surfaces. Their results showed that the bridging fraction and the fraction of adsorbing segments depend explicitly on both energy parameter and the end block size. Haliloglu et al ^[13] have studied the adsorption of symmetric triblock copolymers with sticky end blocks from a nonselective solvent by using Monte Carlo simulations. Their simulation results included the adsorption isotherms and the kinetics of the adsorption.
    From the above brief reviews, it is obvious that there are some progresses on the study of adsorption of triblock copolymers at interface, but the adsorption of triblock copolymer with the middle block sticky has rarely been studied and the size distribution of different configurations is not addressed adequately. In this work, we will focus our attention on the microstructure and adsorption layer information of block copolymer at solid-liquid interface by simulation. The block copolymers are either only one sticky end or two sticky ends or middle-attractive. The density profiles and the size distributions of tail, loop and train configurations are studied. The adsorption information such as the surface coverage and adsorption amount as well as adsorption layer thickness are also presented. The aim is to compare the influence on adsorption behavior at solid-liquid interface by the different sequence of copolymer.

2. PHYSICAL MODEL AND SIMULATION METHOD             
Three types of block copolymers, , and, are investigated in this work.. Block copolymer molecules are modeled as self-avoiding linear chains and in a simple cubic lattice. Each segment of copolymer chain occupies one site and those empty sites are considered to be occupied by solvent molecules S, each of them also occupies one site. The simulations were carried out on a box L_X×L_Y× L_Z=50×50×50 with periodic boundary conditions in the X and Y directions. Two impenetrable hard surfaces located at Z=0 and Z=L_Z+1 and without periodic conditions were introduced in the Z direction. The solvent was taken to be athermal to exclude any self-association. The only nonzero energy term in the simulation was the adsorption energy between attractive segments and surface. The reduced interaction energies between the surface and segments A is . Thus, is a copolymer with two attractive ends, is with one attractive end andis of middle attractive. The simulation algorithm was described in detail in the previous works ^[14-15].
    The number density of chains, F_c, the segment density or concentration at layer Z,, the adsorption amount, G , adsorption layer thickness, s, can be calculated as follows, respectively,
(1)
(2)
(3)
(4)
    where M, N_Z , N_a and r are the number of chains introduced into the simulation box, the number of segments in the Z-th layer, the number of adsorbed chains on a surface and the chain length, respectively, .
    The surface coverage,q , is defined as the segment density or concentration at layer Z=1 or Z=L_Z, i.e. q = f₁ or q = f_Lz. q_A and q_B are the corresponding segment densities of A and B, respectively.
    The bulk concentration, f₀, i.e. the segment density of the region where the concentration of segments is constant among with lattice layers, can be determined by averaging the most intermediate 21 layers because adsorption layers typically extend up to approximately 10 layers away from the surface. The intermediate 21 layers are between 15 and 35 for 50 lattice layers.

3. RESULTS AND DISCUSSIONS
3.1 Size distributions of various configurations of adsorbed block copolymers              
The chains adsorbed usually present in various configurations, which further determine the other adsorption properties. We thus will first present the chain configurations. When the numbers of attractive and non-attractive segments are all fixed, the size distributions of various configurations would have a large difference as expected if the position of attractive blocks in a copolymer chain is different. Size distributions of different configurations for diblock A₁₀B₂₀, triblocks A₅B₂₀A₅ and B₁₀A₁₀B₁₀ for, are exhibited in Figure 1, where (A), (B) and (C) are for tails, trains and loops, respectively.

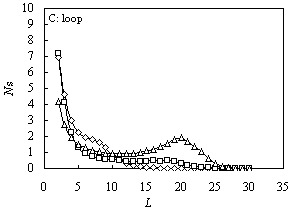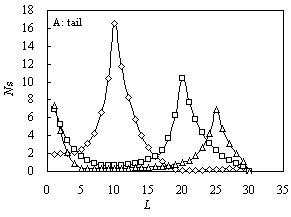
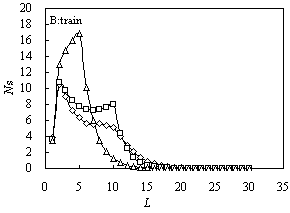
Fig. 1 The size distribution of various configurations for A₁₀B₂₀ (square), A₅B₂₀A₅ (triangle) and B₁₀A₁₀B₁₀ (diamond) for and. A: tail; B: train; C: loop

    The size distributions of tails for the three samples have two peaks as shown in Figure 1(A). For B₁₀A₁₀B₁₀, the first peak appears at L = 10, which just equals to the length of non-attractive block B; the other small one is at L = 29 corresponding to the case when only one segment is adsorbed, where L is the length of configuration. The second peak of B₁₀A₁₀B₁₀ would become larger for smaller energy. However, for A₁₀B₂₀ and A₅B₂₀A₅, the first peak all appears at L = 1, and the second peak of A₁₀B₂₀ is at L =20 while A₅B₂₀A₅ is at L = 25.
    The size distributions of trains for the three samples have a platform, from L =2 to 5 for A₅B₂₀A₅, from L = 2 to 10 for A₁₀B₂₀ and B₁₀A₁₀B₁₀, as shown in Figure 1(B). The platform of A₁₀B₂₀ is higher than that of B₁₀A₁₀B₁₀. With the increasing of L, the distribution curve decreases faster for the former than for the latter. From Figure 1(B), the size distributions of trains are determined by attractive block. The first peak always appears at L=2, the second peak appears at the length of a segment of attractive block; but whether the second peak of train configuration appear or not is determined by energy between segment and surface. If the length is shorter, the emergence of the second peak of trains only needs a small energy.
    The size distributions of loops are shown in Figure 1(C). For A₁₀B₂₀ and B₁₀A₁₀B₁₀, just one peak appears at L = 2, then it will decrease monotonically. For A₅B₂₀A₅, there are two peaks at L = 2 and L = 20, indicating more chance to form bigger loop configuration when both the terminals are attractive.

3.2 Density profiles       
The segment-density profiles of three systems with respect to the distance from the surface,, forand are depicted in Figure 2. Profiles include that of segments A and B. From the figure we can see that segments A form a thin adsorbed layer directly adjacent to the surface by manifesting a maximum density in the first layer. Obviously, this is because of the attractive interaction with the surface enhancing a preferential adsorption. With the increase of distance from the surface, density of segment A decreases very quickly and then increases a little to approach the bulk value. In the first layer, the largest density is achieved by A₁₀B₂₀, then by B₁₀A₁₀B₁₀, and the smallest by A₅B₂₀A₅. With the increasing of distance from the surface, the position of density profiles between A₁₀B₂₀ and A₅B₂₀A₅ would be exchanged, but B₁₀A₁₀B₁₀ is still in the middle.
    Segments B exhibit a low density in the first layer because they are non-attractive. From this figure, we can see that segment B, although non-attractive, can still be adsorbed onto the surface with small adsorption amount due to chain connectivity. The density of segment B then increases with the increment of distance from the surface and reaches a maximum value at several layers away from the surface due to the limitation of chain connectivity. The exact position of the maximum is determined mainly by the position of attractive block located and the length of B block. It is at the 3rd layer for B₁₀A₁₀B₁₀ and A₅B₂₀A₅, and the 4rd layer for A₁₀B₂₀. After the maximum is reached, the density decreases monotonically to the bulk value.

Fig. 2 The density profiles of segment A (open symbol) and segment B (solid symbol) for and. Diamond: A₁₀B₂₀; square: A₅B₂₀A₅; triangle: B₁₀A₁₀B₁₀

3.3 Surface Coverage and Adsorption Isotherms
Figure 3 illustrates surface coverage under other different bulk concentration for A₁₀B₂₀, A₅B₂₀A₅ and B₁₀A₁₀B₁₀ for . From simulation, we found that the surface coverage of segment A for three samples are all increased monotonously with the bulk concentration, when the reduced adsorption energy between segment A and surface is 1.2. However, the relative position is rather different from each other. The upper one is for A₁₀B₂₀, the middle for B₁₀A₁₀B₁₀ and the lower for A₅B₂₀A₅, respectively. If energy is smaller, the surface coverage of A₁₀B₂₀ is usually greater than that of B₁₀A₁₀B₁₀ and A₅B₂₀A₅. The surface coverage for the latter two is nearly the same.
    The value of surface coverage depends also on the relative number of attractive and non-attractive segments. We have also studied two other special series, one is A₁₈B₂, A₉B₂A₉ and B₁A₁₈B₁, and another is A₂B₂₀, A₁B₂₀A₁ and B₁₀A₂B₁₀. The former has a rather shorter non-attractive block and the latter attractive block. For series of A₁₈B₂, A₉B₂A₉ and B₁A₁₈B₁, the difference of surface coverage between each other is not so large and can be neglected. It means that when non-attractive segment block is much shorter than attractive one, the influence of sequence of copolymer on surface coverage is not great. For series of A₂B₂₀, A₁B₂₀A₁ and B₁₀A₂B₁₀, the surface coverage due to segment A is ordered in value from B₁₀A₂B₁₀, A₁B₂₀A₁ to A₂B₂₀ for. If energy is further reached to 1.2, this order would be A₁B₂₀A₁, B₁₀A₂B₁₀ and A₂B₂₀.

Fig. 3 The surface coverage duo to segments A for A₁₀B₂₀ (diamond), A₅B₂₀A₅ (square) and B₁₀A₁₀B₁₀ (triangle) for and.
    Adsorption isotherms for diblock A₁₀B₂₀, triblocks A₅B₂₀A₅ and B₁₀A₁₀B₁₀ are plotted in Figure 4. The adsorption amount increases with the bulk concentration for all systems. It is found that when, the adsorbed amount is greater for the diblock copolymer A₁₀B₂₀ than for the triblock copolymer A₅B₂₀A₅ and B₁₀A₁₀B₁₀. Especially, the adsorbed amount of B₁₀A₁₀B₁₀ is greater than that of A₅B₂₀A₅ if, and the former is even lower than the latter as further increases. The adsorbed amount is ordered in value from B₁₀A₁₀B₁₀, A₅B₂₀A₅ to A₁₀B₂₀ when. However, the difference between A₁₀B₂₀ and A₅B₂₀A₅ is very small.

Fig. 4 The adsorption isotherms for A₁₀B₂₀ (diamond), A₅B₂₀A₅ (square) and B₁₀A₁₀B₁₀ (triangle) forand.
Fig. 5 The adsorption isotherms for A₂B₂₀ (diamond), A₁B₂₀A₁ (square) and B₁₀A₂B₁₀ (triangle) forand.

    For series of A₁₈B₂, A₉B₂A₉ and B₁A₁₈B₁, the adsorbed amount is nearly the same whatever energy is used. This implies that the influence of the sequence of copolymer on adsorbed amount can be neglected. For series of A₂B₂₀, A₁B₂₀A₁ and B₁₀A₂B₁₀, A₂B₂₀ and A₁B₂₀A₁ give nearly the same adsorbed amount which is slightly greater than B₁₀A₂B₁₀ does when. If, the biggest adsorbed amount is achieved by A₂B₂₀, followed by A₁B₂₀A₁ and B₁₀A₂B₁₀ as shown in Figure5. Therefore, the order of adsorbed amount is, and. This conclusion is inconsistent with that of Haliloglu et al¹³, who reckoned that, at low, the adsorbed amount is greater for than for because the surface has a higher chance to meet any one of the two sticky ends belongs to a triblock than only one end of the diblock copolymer chain. However, our simulation results show explicitly that the adsorbed amount is commonly greater for than for. This can be explained as follows:has more chance to form bigger loop configuration when both the two ends are attractive; loop configuration will counteract more attractive segments approaching surface. In other words, a series of loop configurations can lead to screening effects near the interface, and the adsorbed amount then decreases.

3.4 Adsorption layer thickness
The results simulated show that the thickness of tails always greater than that of loop, being independent of the sequence of copolymer. It implies that tails play a more important role in determining the thickness of adsorption layer. The number and size of tails together determine the adsorption layer thickness. The adsorption layer thickness versus bulk concentration is depicted in Figure 6 for different energies for diblock A₁₀B₂₀, triblocks A₅B₂₀A₅ and B₁₀A₁₀B₁₀. Thickness decreases monotonously for three systems, with the increasing of bulk concentration when energy is 0.4. The thickness is the largest for A₅B₂₀A₅ and the smallest for B₁₀A₁₀B₁₀. If energy is 1.2, The thickness first increases quickly and then slowly. In this case, the largest thickness is for A₁₀B₂₀ because A₅B₂₀A₅ forms bigger loop.

Fig. 6 The adsorption layer thickness for A₁₀B₂₀ (diamond), A₅B₂₀A₅ (square) and B₁₀A₁₀B₁₀ (triangle) when (dash line) and (solid line)

    For series of A₂B₂₀, A₁B₂₀A₁ and B₁₀A₂B₁₀, the thickness of A₂B₂₀ and A₁B₂₀A₁ is nearly the same and all greater than that of B₁₀A₂B₁₀ if energy is 0.4. When the energy becomes larger, the thickness is ordered in value from B₁₀A₂B₁₀, A₁B₂₀A₁ to A₂B₂₀. For series of A₁₈B₂, A₉B₂A₉ and B₁A₁₈B₁, whatever energy is used, their thickness has the sequence of order always as B₁A₁₈B₁, A₁₈B₂ and A₉B₂A₉.

4. CONCLUSIONS             
Extensive Monte Carlo simulations on a cubic lattice have been performed to provide a systematic comparison between diblock and triblock copolymer to study the influence of the sequence of copolymer to adsorption behavior. The results simulated show that the position of attractive block in a copolymer chain affects the adsorption behavior.
    It is found that the size distribution of train and tail for, and all may present two peaks. The peak intensity and position are determined by the sequence of copolymer and the reduced adsorption energy. For, bigger loop can be easily formed. The sequence of copolymer affects surface coverage and the adsorbed amount also. The order of adsorbed amount is, and, unless the reduced adsorption energy and the number of non-attractive segments is relatively small. Copolymeralways gives the smallest surface coverage and adsorbed amount as well as adsorbed layer thickness.

REFERENCES
[1] Zhan Y, Mattice W L, Napper D H. J. Chem. Phys., 1993, 98: 7502.
[2] Clancy T C, Webber S E. Macromolecules, 1997, 30:1340.
[3] Wang Y, Li Y, Mattice W L. J. Chem. Phys., 1993,98: 9881.
[4] Wang Y, Li Y, Mattice W L. J. Chem. Phys., 1993,99: 4068.
[5] Wang Y, Teraoka I. Macromolecules, 2000, 33: 3478.
[6] Kim S H, Jo W H. J. Chem. Phys., 1999,110:12193.
[7] Muller M, Schmid F. Annu. Rev. Comput. Phys., 1999, 6: 59.
[8] Geisinger T, Muller M, Binder K. J. Chem. Phys., 1999,111: 5241.
[9] Wang Q, Yan Q, Nealey P F, et al. J. Chem. Phys., 2000, 112: 450.
[10] Balazs A C, Lewandowshi S. Macromolecules, 1990, 23: 839.
[11] Misra S, Mattice W L. Macromolecules, 1994, 27: 2058.
[12] Nguyen-Misra M, Misra S, Mattice W L. Macromolecules, 1996, 29:1407.
[13] Haliloglu T, Stevenson D C, Mattice W L. J. Chem. Phys., 1997, 106: 3365.
[14] Jiang J W, Liu H L, Hu Y. Macrom. Theory Simul., 1998, 7: 113.
[15] Chen T, Liu H L, Hu Y. J. Chem. Phys., 2001, 114: 5937.

[ Back ] [ Home ] [ Up ] [ Next ]Mirror Site in USA  Europe  China  GBNet