http://www.chemistrymag.org/cji/2003/056047pe.htm |
Jun. 1, 2003 Vol.5 No.6 P.47 Copyright |
Zhang Shuwen, Ba Xinwu, Han Yinghui,
Wang Sujuan, Wang Haijun
(College of Chemistry & Environmental Science, Hebei University, Baoding 071002,
China)
Abstract By means of kinetic
differential equation approach, the mean square radius of gyration of the hyperbranched
polymers formed by self-condensing vinyl polymerization was investigated explicitly.
Averaged over the molecular weight distribution, the explicit expressions of the number-,
weight- and z-average mean square radii of gyration are given as a function of conversion
of double bonds, in which the contribution of the unreacted monomers in the hyperbranched
polymer systems is included and excluded, respectively. The variation of the average size
of the hyperbranched polymers during the self-condensing vinyl polymerization can be
predicted to conclude that the weight- and the z-average mean square radii of gyration
increase sharply at the end of reaction, which enlarge over ten times as the conversion of
double bonds rises from 0.99 to 0.999.
Keywords Hyperbrabched polymer, radius of gyration, self-condensation vinyl polymerization
1. INTRODUCTION
Hyperbranched polymers have received considerable attention in recent year partly because
they do show properties very similar to dendrimers (e.g. high functionality, low
viscosity, and so on), which are of particular interest for the utilization in catalysis,
supermolecular chemistry and biochemistry, [1] and their syntheses are much
simpler than those of dendrimers. [2,3] In 1995 Frechet and co-workers reported
a new way of forming hyperbranched polymers based on vinyl monomers and named it as
"self-condensation vinyl polymerization" (SCVP).
[4] Since then living cationic,[4] nitroxide-mediated radical, [5]
atom transfer radical, [6] and group transfer polymerizations [7]
have been applied to the synthesis of hyperbranched polymers. The theoretical description
of SCVP leading to hyperbranched polymers was proposed by Muller and Yan to give the
molecular weight distribution, the branching density and the other characteristic mean
values. [8,9] As it is well known, the physical properties of polymer materials
depend crucially on molecular parameters, such as the molecular number distribution, the
average molecular weight, the branching density, the mean square end-to-end distance and
the mean square radius of gyration and so on. [12-16] The mean square
end-to-end distance and the mean square radius of gyration are the two most important
values in conformational statistics of polymer chains. For branched or hyperbranched
polymer systems, only the mean square radius of gyration is meaningful. From the
architecture of a hyperbranched polymer, one can see that the mean square radius of
gyration is smaller than that of a linear polymer chain of the same molecular weight due
to the branching effect. The mean square radius of gyration can be averaged over the
molecular weight distribution to give the average mean square radius of gyration, which
increases as the conversion of functional groups or reaction time, and is experimentally.
For example, the z-average mean square radius of gyration is generally determined from
light scattering experiments. [16] Experimental measurement of the structure
functions at small momentum transfer can yield the z-average mean square radius of
gyration varying with the conversion of groups or reaction time, and therefore
understanding the variation of the average mean square radius of gyration with the
conversion or reaction time may help to improve present knowledge about the architecture
of the elementary structure and formation kinetic. From the theoretical point of view,
there are two methods being used to calculate the average mean square radius of gyration.
One is the computer simulation based on the formation kinetic, which is not discussed in
detail in this paper. [19, 20] Another is the analytical technique, such as the
statistical method, [13, 14] stochastic theory of branching processes, [15]
the kinetic approach method [17,18] and so on. It should be point out, to our
knowledge, that no analytical technique has been proposed to give the conversion
dependence of the average mean square radius of gyration during the self-condensing vinyl
polymerization.
In this paper, we focus our attention on the conversion dependence of
the average mean square radius of gyration for hyperbranched polymers systems generated by
self-condensing vinyl polymerization. We will first give a brief review of the kinetic
differential equation approach and the concentration of n-mer Pn,
[8] and then a decomposition formula for the combinatorial coefficient of the
concentration of n-mer will be proposed. The statistical interpretation of this
formula, which is similar to the argument proposed by Dobson, Gordon [15] and
some of the authors [17,18] for the branched polymers, is shown in detail to
give the mean square radius of gyration. Finally, we will give the analytical expressions
of the number-, weight- and z-average mean square radii of gyration dependence on the
conversion of double bonds, in which the contribution of the unreacted monomers in the
hyperbranched polymer systems is included and excluded, respectively.
2. THE MEAN SQUARE RADIUS OF GYRATION
According to the reaction scheme proposed by Muller and Yan, the kinetic differential
equation and chemical kinetic equation for self-condensing vinyl polymerization can be
given as [8,9]
![]() (1)
(1)
![]() (2)
(2)
where Pn is the concentration of n-mers, x is the
conversion of double bonds, W0 is initial concentration in the reaction
system, and k is the effective rate constant of the reaction. In obtaining above
equation, the assumptions of ideal network polymerization were retained, i.e., all
functional groups of the same type are equally reactive, all groups react independently,
and no intramolecular reactions occur in finite species. With the initial condition ![]() , where
, where![]() is Kronecker symbol, the concentrations of n-mers can be derived as
[9]
is Kronecker symbol, the concentrations of n-mers can be derived as
[9]
![]() (3)
(3)
with
![]() (4)
(4)
where Cn is the combinatorial coefficient.
Let us now give a decomposition formula of the combinatorial
coefficient Cn. Dividing Eq.(1) by Eq.(2), one can obtain
![]() (5)
(5)
Substituting the concentration of the n-mer Pn
given by Eq.(3) into Eq.(5), a decomposition formula for the combinatorial coefficient Cn
can be given
![]() (6)
(6)
In order to give the statistical interpretation of Eq.(6) more clearly, we may rewrite it
in symmetric form
![]() (7)
(7)
with
![]() (8)
(8)
For an arbitrary n-mer in the ensemble of molecules, there may
be in general (n-1) bonds formed during the polymerization process without
consideration of the intramolecular reaction. Considering an arbitrary bond in the n-mer,
where the monomers are defined as the mass points for simplicity, there may be two
moieties if this bond is imagined to be cut. The number of mass points found in the two
moieties of molecule produced by cutting this bond is i and (n-i)
respectively. From Eqs.(7) and (8), we see that the term n-1 on the left side
is the number of bonds in a n-mer, and the term D(n.i) on the right
side should be the number of bonds whose splitting produces two moieties of i and (n-i)
mass points. The summation in Eq.(8) with respect to i gives the total number of
bonds in the n-mer.
Next the mean square radius of gyration for the hyperbranched polymers
is calculated with aid of a decomposition formula given by Eq.(7). The square radius of
gyration for a hyperbranched polymer consisting of n mass points with fixed
conformation is defined as
![]() (9)
(9)
where ri is the distance of the i-th mass point from the center
of gravity of the molecule. A simple argument, proposed by Zimm and Stockmayer leads to
the transformation 14
![]() (10)
(10)
where rij is the distance from the i-th mass point to the j-th
one. With cyclic molecules being excluded, there is a unique path of bonds leading from i-th
mass point to the j-th one in the n-mer, in which the number of bonds on the
path can be varied from 1 to (n-1). The mean square radius of gyration ![]() , which averages the fluctuations in time of
, which averages the fluctuations in time of ![]() due to Brownian motion, can be expressed as
due to Brownian motion, can be expressed as
![]() (11)
(11)
Using the method proposed by Dobson and Gordon [15], the
mean square radius of gyration ![]() in
Eq.(14) can be reformulated as
in
Eq.(14) can be reformulated as
![]() (12)
(12)
where b is the effective bond length. It should be noted that the assumption of all
bond lengths in a hyperbranched polymer being equal was taken. The index h in the
summation is used to denote the h-th bond in the n-mer. The term ![]() and
and ![]() on the right hand side of Eq.(12) are the number of mass points
associated with the two moieties which produced by imaginary cutting the h-th bond
in the n-mer. The summation runs over all the bonds in the n-mer. As being
mentioned above,
on the right hand side of Eq.(12) are the number of mass points
associated with the two moieties which produced by imaginary cutting the h-th bond
in the n-mer. The summation runs over all the bonds in the n-mer. As being
mentioned above, ![]() in Eq.(8) is the number of
bonds whose splitting produced moieties of i and (n-i) mass points,
respectively. Then the mean square radius of gyration in Eq.(12) can be expressed as
in Eq.(8) is the number of
bonds whose splitting produced moieties of i and (n-i) mass points,
respectively. Then the mean square radius of gyration in Eq.(12) can be expressed as
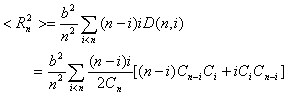 (13)
(13)
The summation in Eq.(13) with respect to i means that splitting
the n-mer produces two moieties of i and (n-i) mass points,
respectively. Since the number of mass points in those two moieties varies from 1 to
(n-1), the summation in Eq.(13) contains all the moieties with different
number of units.
3. THE AVERAGE MEAN SQUARE RADII OF
GYRATION
For most majority synthesis of hyperbranched polymer systems, many different isomeric
structures and a broad molecular weight distribution for hyperbranched polymers are
obtained. Therefore only the average statistical parameters, for instance, z-average mean
square radius, can be measured by light scattering techniques. [16] In order to
calculate the average mean square radii of gyration, the number-, weight- and
z-distribution of the hyperbranched polymers was defined as [9]
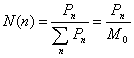 (14)
(14)
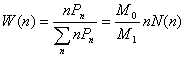 (15)
(15)
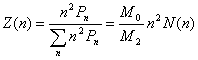 (16)
(16)
where ![]()
![]() are the polymer moments defined as
are the polymer moments defined as
![]() ,
, ![]() ,
,![]() (17)
(17)
The first polymer moment ![]() is the material
balance condition.
is the material
balance condition.
With the aid of the mean square radius of gyration in Eq.(13), the
number-, weight- and z-average mean square radii of gyration for hyperbranched polymer
systems can be defined as follows
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
where ![]() is defined as
is defined as
![]() (21)
(21)
Substituting the mean square radius of gyration ![]() in Eq.(13) and number distribution N(n)
in Eq.(14) into Eq.(21), and letting k=2, the quantity
in Eq.(13) and number distribution N(n)
in Eq.(14) into Eq.(21), and letting k=2, the quantity ![]() can be obtained by means of direct summation
can be obtained by means of direct summation
![]() (22)
(22)
Unfortunately, the two quantities![]() and
and ![]() cannot be evaluated
analytically by means of direct summation. Since the mean square radius of gyration
cannot be evaluated
analytically by means of direct summation. Since the mean square radius of gyration ![]() in Eq.(13) is independent of the conversion of
double bonds x, we can choose x as a variable to differentiate both the right and left
sides of Eq.(21). Letting k=1 yields
in Eq.(13) is independent of the conversion of
double bonds x, we can choose x as a variable to differentiate both the right and left
sides of Eq.(21). Letting k=1 yields
![]() (23)
(23)
Substituting quantity ![]() in Eq.(22) into the above equation
yields
in Eq.(22) into the above equation
yields
![]() (24)
(24)
With the boundary condition ![]() for x=0, the
quantity
for x=0, the
quantity ![]() is obtained by direct solution of
the above differential equation
is obtained by direct solution of
the above differential equation
![]() (25)
(25)
Consecutively, the quantity ![]() can be
calculated in the same manner as that of quantity
can be
calculated in the same manner as that of quantity ![]() . Since the calculation procedure is straightforward, here we only give the
result as follows
. Since the calculation procedure is straightforward, here we only give the
result as follows
![]() (26)
(26)
Using the above results in Eq.(22), (25), (26) and the polymer moments in Eq.(17), the
number-, weight- and z-average mean square radii in Eq.(18)-(20) can be given
explicitly
![]() (27)
(27)
![]() (28)
(28)
![]() (29)
(29)
The results given by Eq.(27)-(29) can be used to predict the variation
of the average size of the hyperbranched polymers during the self-condensation vinyl
polymerization.
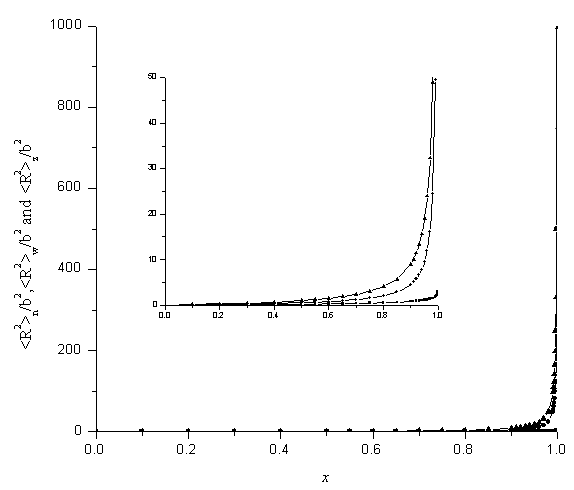
Figure 1. Dependence of the average mean squre radii of gyration on x
¡ö: ![]() ¡ñ:
¡ñ:![]() ¡ø:
¡ø:![]()
Figure 1 shows the numerical calculations of
the average mean square radii of gyration as function of conversion of double bonds, x.
It can be seen that the average mean square radii of gyration increase much more slowly at
the beginning of the reaction, and increase sharply at the end of reaction. The weight-
and z-average mean square radii of gyration increase over ten times as the conversion of
double bonds rise from 0.99 to 0.999. In fact the average mean square radii of gyration
reach infinite when the conversions of double bonds are near the maximum value x=1. The
results also show that the number average mean square radius of gyration ![]() increases slowly than the weight- and the
z-average mean square radii of gyration as the conversion of the double bonds increases,
since the former is divergent as the logarithmic function. The hyperbranched polymers can
be prepared by polymerization of ABf type monomers, where A and B
are two different functional groups capable of reacting with each other, and f is
the number of B groups. [2,3] Here we make the comparison between
z-average mean square radius of gyration of the hyperbranched polymers obtained from the
self-condensation vinyl polymerization with that produced in a polycondensation of AB2
type monomers. The z-average mean square radius of gyration of the hyperbranched polymers
formed by AB2 type polycondensation was given as [18]
increases slowly than the weight- and the
z-average mean square radii of gyration as the conversion of the double bonds increases,
since the former is divergent as the logarithmic function. The hyperbranched polymers can
be prepared by polymerization of ABf type monomers, where A and B
are two different functional groups capable of reacting with each other, and f is
the number of B groups. [2,3] Here we make the comparison between
z-average mean square radius of gyration of the hyperbranched polymers obtained from the
self-condensation vinyl polymerization with that produced in a polycondensation of AB2
type monomers. The z-average mean square radius of gyration of the hyperbranched polymers
formed by AB2 type polycondensation was given as [18]
![]() (30)
(30)
where y is the conversion of the A groups.
Figure 2 shows the numerical calculations of the z-average mean square
radii of gyration, ![]() and
and ![]() , as function of the conversions. It can be seen
that the difference between the two quantities is smaller than 1.0% when the conversions
is over 0.99. As the conversions are near the maximum value, x=1 and y=1, the two
quantities have the same asymptotic behavior.
, as function of the conversions. It can be seen
that the difference between the two quantities is smaller than 1.0% when the conversions
is over 0.99. As the conversions are near the maximum value, x=1 and y=1, the two
quantities have the same asymptotic behavior.
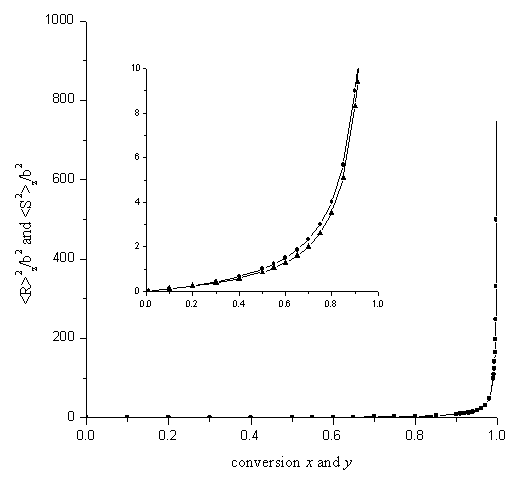
Figure 2. Dependence of the z-average mean
square radii of gyration,![]() and
and ![]() on the conversions
on the conversions
¡ñ: ![]() ¡ø:
¡ø: ![]()
In the experimental procedure, the low molecular weight materials, such
as residual monomer etc., are usually separated from the polymer systems by precipitation.
The number-, weight- and z-distribution of the hyperbranched polymer systems without the
unreacted monomers take the forms
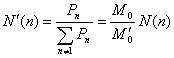 (31)
(31)
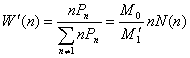 (32)
(32)
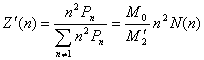 (33)
(33)
with
![]()
![]()
![]() (34)
(34)
where ![]() ,
, ![]() and
and![]() are the polymer moments
without the unreacted monomers. The number-, weight- and z-average mean square radii of
gyration without the unreacted monomers can be evaluated as
are the polymer moments
without the unreacted monomers. The number-, weight- and z-average mean square radii of
gyration without the unreacted monomers can be evaluated as
![]() (35)
(35)
![]() (36)
(36)
![]() (37)
(37)
With the aid of the number distribution given by Eq.(14) and the polymer moments without
the unreacted monomers given by Eq.(34), the average mean square radii of gyration without
unreacted monomers can be given as
![]() (38)
(38)
![]() (39)
(39)
![]() (40)
(40)
Furthermore, the contribution of the low molecular weight materials, such as dimer etc.,
to the average mean square radii can also be calculated without difficulty, and are
omitted in the present paper.
4. SUMMARY AND CONCLUSIONS
From the chemical kinetic equation given by Eq.(2), and branching density definition which
is important parameter characterized the topological structure of hyperbranched polymers,
[8-10] the conversion of double bonds, x, can be easily derived as a
function of the reaction time, or the branching density. The conversion of double bonds,
x, as well as reaction time and branching density, can be measured by means of NMR and
FTIR and other techniques. [4-7] The z-average mean square radius of gyration
is generally determined from light scattering experiments. Thus, our results are
convenient to compare with the experimental data since all quantities in the formulas are
experimentally accessible.
The results obtained in the paper were compared with that produced by
the polycondensation of AB2 type monomers. The numerical calculations showed
that the difference between the two quantities is smaller than 1.0% when the conversions
is over 0.99, and the same asymptotic behavior were also given as the conversions are near
the maximum value, x=1 and y=1. Although the topological structures of the hyperbranched
polymer and dendrimer are similar, but the branching density of the hyperbranched polymer
is smaller than that of the dendrimer, where the branching density has the value 1.0 for
the latter, so a number of linear units exist inside the hyperbranched polymer skeleton.
This means that the molecular weight, as well as the mean square radius of gyration, of
the hyperbranched polymers increases without limitation as the conversion of function
group increase, and the mean square radius of gyration is larger than that of the
dendrimer of the same molecular weight.
The explicit expressions of the average mean square radii of gyration
obtained in this work are based on the assumptions of the statistical ideal network
polymerization, which is the basic model used to describe the polymerization process, and
may not be fulfilled in reality, [9, 11] and therefore certain deviations are
to be expected when comparing with experimental results. The average mean square radii of
gyration can be evaluated by means of the computer simulation technique whenever
statistical non-ideal network polymerization is taken into consideration.[9, 10, 20]
The analytic results in the paper presented an effective way of understanding the physical
properties of hyperbranched polymers during coagulations, and can be used to examine
whether or not the simulation is correct for a given model.
Acknowledgment. This work was supported by the National Natural Science Foundation
(20174008) and the Foundation for University Key Teacher by the Ministry of Education
(680) of China.
REFERENCES
[1] Bosman A W, Janssen H M, Meijer E W. Chem. Rev., 1999, 99: 1665.
[2] Kim Y H, Webster O W. Polym. Prepr. (Am. Chem. Soc., Div. Polym. Chem.), 1988, 29 (2):
1.
[3] Voit B I. Acta Polym., 1995, 46: 87.
[4] Frechet J M J, Henmi M, Gitsobv I et al. Science, 1995, 269: 1080.
[5] Hawker C J, Frechet J M J, Grubbs R B et al. J. Am. Chem. Soc., 1995, 117: 10763.
[6] Gaynor S G, Edelman S, Matyjaszewski K. Macromolecules, 1996, 29, 1079.
[7] Simon P F W, Radke W, Müller A H E. Polym. Prepr.(Am. Chem. Soc., Div. Polym.
Chem.), 1997, 38, 498.
[8] Muller A H E, Yan D, Wulkow M. Macromolecules, 1997, 30: 7015.
[9] Yan D, Muller A H E, Matyjaszewski K. Macromolecules, 1997, 30: 7024.
[10] Simon P F W, Muller A H E. Macromol. Theory and Simul., 2000, 9: 621.
[11] Galina H, Szustalewicz A. Macromolecules. 1990, 23: 3833.
[12] Beginn U, Drohmann C, Moller M. Macromolecules, 1997, 30: 4112.
[13] Stockmayer W H. J. Chem. Phys., 1943, 11, 45. 1944, 12, 125. 1950, 18, 58.
[14] Zimm B H, Stockmayer W H. J. Chem. Phys., 1949, 17: 1301.
[15] Gordon M. Proc. R. Soc. London 1963, A268, 240.
[16] Burchard W. Adv. Polym. Sci., 1983, 48, 1.
[17] Li Z S, Ba X W, Sun C C et al. Macromolecules, 1991, 24: 3696.
[18] Ba X, Wang H, Zhao M et al. Macromolecules, 2002, 35: 3306.
[19] Hanselmann R, Holter D, Frey H. Macromolecules 1998, 31: 3790.
[20] Cameron C, Fawcett A H, Hetherington C R et al. Macromolecules, 2000, 33: 6551.